Question Number 104134 by bemath last updated on 19/Jul/20
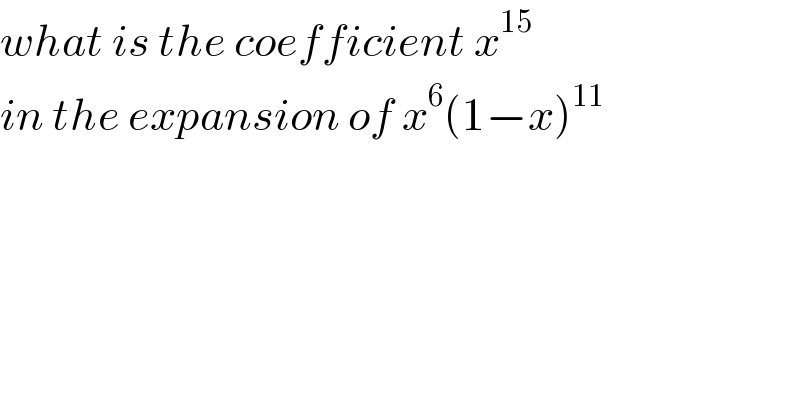
$${what}\:{is}\:{the}\:{coefficient}\:{x}^{\mathrm{15}} \\ $$$${in}\:{the}\:{expansion}\:{of}\:{x}^{\mathrm{6}} \left(\mathrm{1}−{x}\right)^{\mathrm{11}} \\ $$
Answered by bobhans last updated on 19/Jul/20
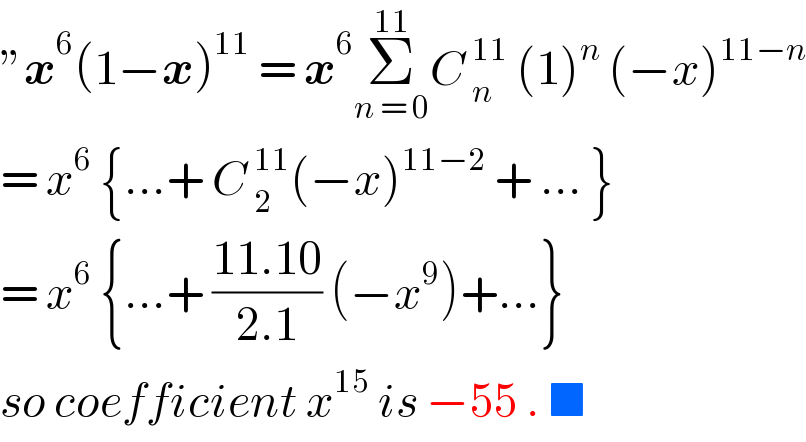
$$''\boldsymbol{{x}}^{\mathrm{6}} \left(\mathrm{1}−\boldsymbol{{x}}\right)^{\mathrm{11}} \:=\:\boldsymbol{{x}}^{\mathrm{6}} \underset{{n}\:=\:\mathrm{0}} {\overset{\mathrm{11}} {\sum}}{C}\:_{{n}} ^{\mathrm{11}} \:\left(\mathrm{1}\right)^{{n}} \:\left(−{x}\right)^{\mathrm{11}−{n}} \\ $$$$=\:{x}^{\mathrm{6}} \:\left\{…+\:{C}\:_{\mathrm{2}} ^{\mathrm{11}} \left(−{x}\right)^{\mathrm{11}−\mathrm{2}} \:+\:…\:\right\} \\ $$$$=\:{x}^{\mathrm{6}} \:\left\{…+\:\frac{\mathrm{11}.\mathrm{10}}{\mathrm{2}.\mathrm{1}}\:\left(−{x}^{\mathrm{9}} \right)+…\right\} \\ $$$${so}\:{coefficient}\:{x}^{\mathrm{15}} \:{is}\:−\mathrm{55}\:.\:\blacksquare\: \\ $$
Answered by mathmax by abdo last updated on 19/Jul/20
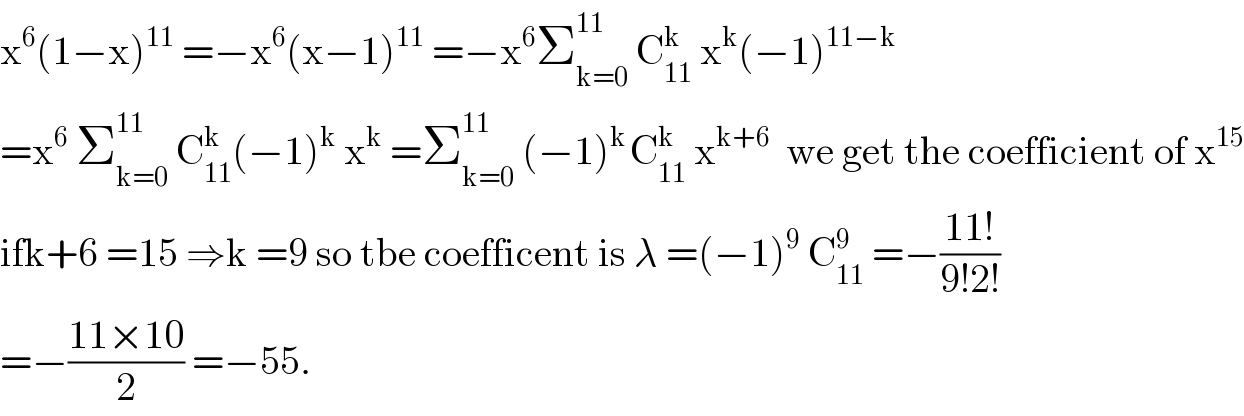
$$\mathrm{x}^{\mathrm{6}} \left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{11}} \:=−\mathrm{x}^{\mathrm{6}} \left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{11}} \:=−\mathrm{x}^{\mathrm{6}} \sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{11}\:} \:\mathrm{C}_{\mathrm{11}} ^{\mathrm{k}} \:\mathrm{x}^{\mathrm{k}} \left(−\mathrm{1}\right)^{\mathrm{11}−\mathrm{k}} \\ $$$$=\mathrm{x}^{\mathrm{6}} \:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{11}} \:\mathrm{C}_{\mathrm{11}} ^{\mathrm{k}} \left(−\mathrm{1}\right)^{\mathrm{k}} \:\mathrm{x}^{\mathrm{k}} \:=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{11}} \:\left(−\mathrm{1}\right)^{\mathrm{k}\:} \mathrm{C}_{\mathrm{11}} ^{\mathrm{k}} \:\mathrm{x}^{\mathrm{k}+\mathrm{6}} \:\:\mathrm{we}\:\mathrm{get}\:\mathrm{the}\:\mathrm{coefficient}\:\mathrm{of}\:\mathrm{x}^{\mathrm{15}} \\ $$$$\mathrm{ifk}+\mathrm{6}\:=\mathrm{15}\:\Rightarrow\mathrm{k}\:=\mathrm{9}\:\mathrm{so}\:\mathrm{tbe}\:\mathrm{coefficent}\:\mathrm{is}\:\lambda\:=\left(−\mathrm{1}\right)^{\mathrm{9}} \:\mathrm{C}_{\mathrm{11}} ^{\mathrm{9}} \:=−\frac{\mathrm{11}!}{\mathrm{9}!\mathrm{2}!} \\ $$$$=−\frac{\mathrm{11}×\mathrm{10}}{\mathrm{2}}\:=−\mathrm{55}. \\ $$
