Question Number 115908 by Eric002 last updated on 29/Sep/20
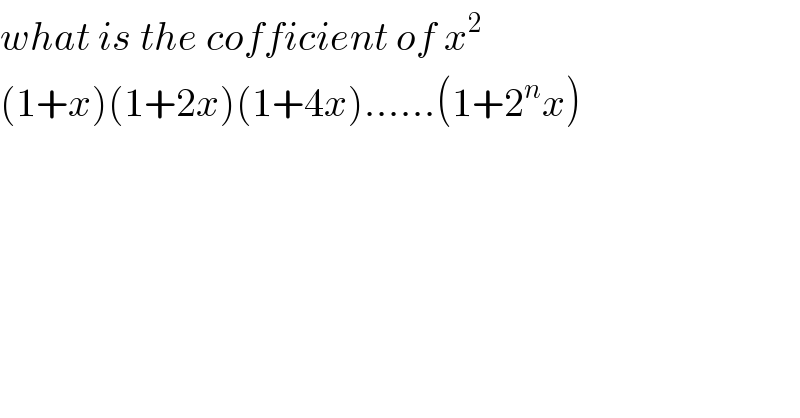
$${what}\:{is}\:{the}\:{cofficient}\:{of}\:{x}^{\mathrm{2}} \\ $$$$\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+\mathrm{2}{x}\right)\left(\mathrm{1}+\mathrm{4}{x}\right)……\left(\mathrm{1}+\mathrm{2}^{{n}} {x}\right) \\ $$
Commented by soumyasaha last updated on 29/Sep/20
![Coefficient = (1/2)[ (Σ_(r=0) ^n 2^r )^2 − Σ_(r=0) ^n (2^r )^2 ] = (1/2)[ (2^(n+1) −1)^2 − (1/3)(4^(n+1) −1)]](https://www.tinkutara.com/question/Q115937.png)
$$ \\ $$$$\:\mathrm{Coefficient}\:=\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}\left[\:\left(\underset{\mathrm{r}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\mathrm{2}^{\mathrm{r}} \right)^{\mathrm{2}} −\:\underset{\mathrm{r}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\left(\mathrm{2}^{\mathrm{r}} \right)^{\mathrm{2}} \right] \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left[\:\left(\mathrm{2}^{\mathrm{n}+\mathrm{1}} −\mathrm{1}\right)^{\mathrm{2}} −\:\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{4}^{\mathrm{n}+\mathrm{1}} −\mathrm{1}\right)\right] \\ $$$$ \\ $$
Commented by prakash jain last updated on 29/Sep/20

$$\mathrm{Thanks} \\ $$
Answered by mr W last updated on 29/Sep/20
![(1/2)Σ_(k=0) ^n 2^k Σ_(i=0≠k) ^n 2^i =(1/2)Σ_(k=0) ^n 2^k (Σ_(i=0) ^n 2^i −2^k ) =(1/2)Σ_(k=0) ^n 2^k (((2^(n+1) −1)/(2−1))−2^k ) =(1/2)Σ_(k=0) ^n 2^k (2^(n+1) −1−2^k ) =(1/2)(2^(n+1) −1)Σ_(k=0) ^n 2^k −(1/2)Σ_(k=0) ^n 4^k =(1/2)(2^(n+1) −1)(2^(n+1) −1)−(1/2)×((4^(n+1) −1)/(4−1)) =(1/2)[2^(2(n+1)) −2×2^(n+1) +1]−((2^(2(n+1)) −1)/(2×3)) =((2(2^(2n+1) +1))/3)−2^(n+1) example n=2: =((2(2^5 +1))/3)−2^3 =14](https://www.tinkutara.com/question/Q115947.png)
$$\frac{\mathrm{1}}{\mathrm{2}}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\mathrm{2}^{{k}} \underset{{i}=\mathrm{0}\neq{k}} {\overset{{n}} {\sum}}\mathrm{2}^{{i}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\mathrm{2}^{{k}} \left(\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}\mathrm{2}^{{i}} −\mathrm{2}^{{k}} \right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\mathrm{2}^{{k}} \left(\frac{\mathrm{2}^{{n}+\mathrm{1}} −\mathrm{1}}{\mathrm{2}−\mathrm{1}}−\mathrm{2}^{{k}} \right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\mathrm{2}^{{k}} \left(\mathrm{2}^{{n}+\mathrm{1}} −\mathrm{1}−\mathrm{2}^{{k}} \right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}^{{n}+\mathrm{1}} −\mathrm{1}\right)\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\mathrm{2}^{{k}} −\frac{\mathrm{1}}{\mathrm{2}}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\mathrm{4}^{{k}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}^{{n}+\mathrm{1}} −\mathrm{1}\right)\left(\mathrm{2}^{{n}+\mathrm{1}} −\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{4}^{{n}+\mathrm{1}} −\mathrm{1}}{\mathrm{4}−\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{2}^{\mathrm{2}\left({n}+\mathrm{1}\right)} −\mathrm{2}×\mathrm{2}^{{n}+\mathrm{1}} +\mathrm{1}\right]−\frac{\mathrm{2}^{\mathrm{2}\left({n}+\mathrm{1}\right)} −\mathrm{1}}{\mathrm{2}×\mathrm{3}} \\ $$$$=\frac{\mathrm{2}\left(\mathrm{2}^{\mathrm{2}{n}+\mathrm{1}} +\mathrm{1}\right)}{\mathrm{3}}−\mathrm{2}^{{n}+\mathrm{1}} \\ $$$$ \\ $$$${example}\:{n}=\mathrm{2}: \\ $$$$=\frac{\mathrm{2}\left(\mathrm{2}^{\mathrm{5}} +\mathrm{1}\right)}{\mathrm{3}}−\mathrm{2}^{\mathrm{3}} =\mathrm{14} \\ $$
