What-is-the-common-formula-to-obtain-the-3-solutions-of-a-polynomial-equation-in-the-following-form-ax-3-b-2-x-cx-d-0-

Question Number 56368 by Hassen_Timol last updated on 15/Mar/19

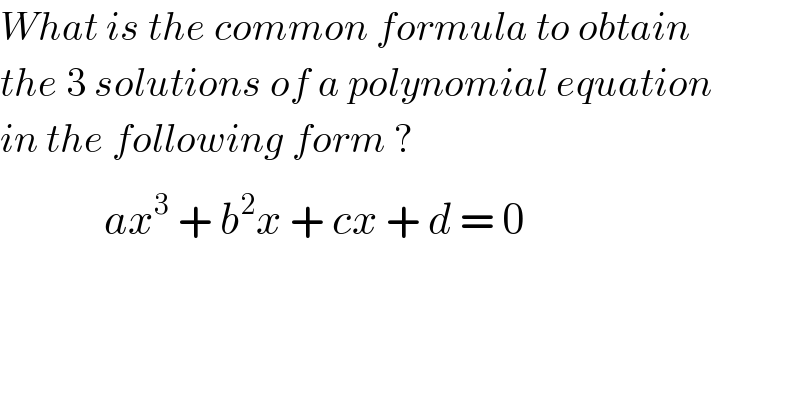
W h a t i s t h e c o m m o n f o r m u l a t o o b t a i n

t h e 3 s o l u t i o n s o f a p o l y n o m i a l e q u a t i o n

i n t h e f o l l o w i n g f o r m ?

{a x}^{3} + b^{2} x + c x + d = 0

Commented by mr W last updated on 15/Mar/19

Commented by Hassen_Timol last updated on 16/Mar/19

T h a n k y o u s o m u c h!!!!!

Answered by MJS last updated on 15/Mar/19

1 . divide by a

x^{3} + \frac{b}{a} x^{2} + \frac{c}{a} x + \frac{d}{a} = 0

2 . substitute x = z - \frac{b}{3 a}

z^{3} + \frac{3 a c - b^{2}}{3 a^{2}} z + \frac{27 a^{2} d - 9 a b c + 2 b^{3}}{27 a^{3}} = 0

3 . substitute \frac{3 a c - b^{2}}{3 a^{2}} = p; \frac{27 a^{2} d - 9 a b c + 2 b^{3}}{27 a^{3}} = q

z^{3} + p z + q = 0

4 . check resolvability

D = \frac{p^{3}}{27} + \frac{q^{2}}{4}

D ⩾ 0 \Rightarrow {Cardano}^{'} s formula

D < 0 \Rightarrow trigonometric formula

5 . solve

Cardano :

u = \sqrt[3]{- \frac{q}{2} + \sqrt{\frac{p^{3}}{27} + \frac{q^{2}}{4}}}; v = \sqrt[3]{- \frac{q}{2} - \sqrt{\frac{p^{3}}{27} + \frac{q^{2}}{4}}}

{it}^{'} s essential to take the principal 3^{rd} root

z_{1} = u + v

z_{2} = (- \frac{1}{2} - \frac{\sqrt{3}}{2} i) u + (- \frac{1}{2} + \frac{\sqrt{3}}{2} i) v

z_{3} = (- \frac{1}{2} + \frac{\sqrt{3}}{2} i) u + (- \frac{1}{2} - \frac{\sqrt{3}}{2} i) v

trigonometric :

z_{n} = \frac{2}{3} \sqrt{- 3 p} \sin (\frac{2 π}{3} n + \frac{1}{3} \arcsin \frac{3 \sqrt{3} q}{2 \sqrt{- p^{3}}}) with n = 1, 2, 3

Commented by Hassen_Timol last updated on 16/Mar/19

T h a n k s a l o t \dots

Commented by mr W last updated on 16/Mar/19

v e r y n i c e s u m m a r y! t h a n k s s i r!

Facebook Tweet Pin