Question Number 104280 by Anindita last updated on 20/Jul/20

$$\boldsymbol{\mathrm{What}}\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{GCD}}\:\boldsymbol{\mathrm{of}}\: \\ $$$$\frac{\mathrm{1}}{\mathrm{2}},\:\frac{\mathrm{3}}{\mathrm{4}},\:\frac{\mathrm{16}}{\mathrm{30}}\:? \\ $$
Commented by 1549442205PVT last updated on 20/Jul/20
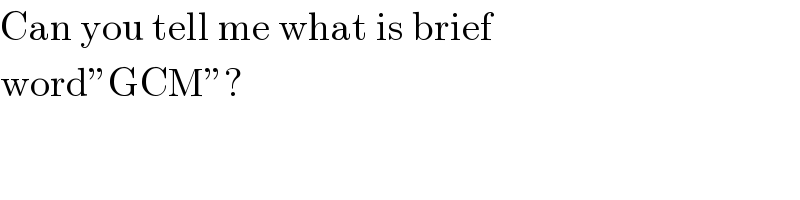
$$\mathrm{Can}\:\mathrm{you}\:\mathrm{tell}\:\mathrm{me}\:\mathrm{what}\:\mathrm{is}\:\mathrm{brief} \\ $$$$\mathrm{word}''\mathrm{GCM}''? \\ $$
Commented by bramlex last updated on 20/Jul/20
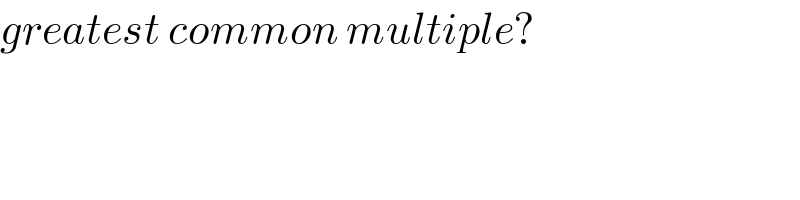
$${greatest}\:{common}\:{multiple}? \\ $$
Commented by Anindita last updated on 20/Jul/20

$$\mathrm{Yes} \\ $$
Commented by Rasheed.Sindhi last updated on 20/Jul/20

$${Perhaps}\:{you}\:{mean}\:\mathrm{LCM}\: \\ $$$$\left({least}\:{common}\:{multiple}\right)\:{or} \\ $$$$\mathrm{GCD}\left({greatest}\:{common}\right. \\ $$$$\left.{divisor}\right). \\ $$
Commented by 1549442205PVT last updated on 21/Jul/20
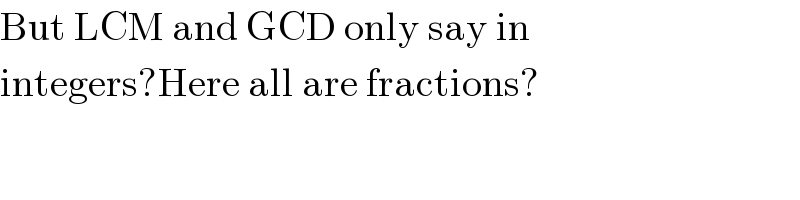
$$\mathrm{But}\:\mathrm{LCM}\:\mathrm{and}\:\mathrm{GCD}\:\mathrm{only}\:\mathrm{say}\:\mathrm{in} \\ $$$$\mathrm{integers}?\mathrm{Here}\:\mathrm{all}\:\mathrm{are}\:\mathrm{fractions}? \\ $$
Answered by Rasheed.Sindhi last updated on 24/Jul/20

$${LCM}\:{of}\:{denominators}=\mathrm{60} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{30}}{\mathrm{60}}\:,\:\frac{\mathrm{3}}{\mathrm{4}}=\frac{\mathrm{45}}{\mathrm{60}}\:,\frac{\mathrm{16}}{\mathrm{30}}=\frac{\mathrm{32}}{\mathrm{60}} \\ $$$${Now}\:{GCD}\:{of}\:{numerators} \\ $$$$\mathrm{30},\mathrm{45},\mathrm{32}\:=\mathrm{1} \\ $$$${So}\:\mathrm{GCD}\:{of}\:{the}\:{given}\:{fractions} \\ $$$$\:{is}\:\:\frac{\mathrm{1}}{\mathrm{60}}\: \\ $$$$\left({We}\:{have}\:\mathrm{30}\:{sixtieths},\mathrm{45}\:{sixtieths}\right. \\ $$$$\&\:\mathrm{32}\:{sixtieths}.{You}\:{can}\:{see}\:{that} \\ $$$$\mathrm{1}\:{sixtieth}\left(\mathrm{1}/\mathrm{60}\right)\:{is}\:{a}\:{common}\: \\ $$$${divisor}\:{and}\:{it}'{s}\:{also}\:{greatest} \\ $$$${common}\:{divisor},{b}/{c}\:{there}\:{is}\:{no} \\ $$$$\left.{common}\:{divisor}\:{greater}\:{than}\:{this}.\right) \\ $$
