Question Number 98098 by bobhans last updated on 11/Jun/20
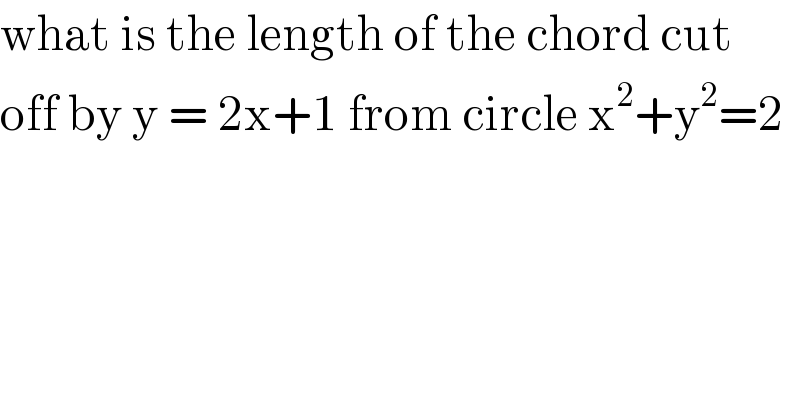
$$\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{length}\:\mathrm{of}\:\mathrm{the}\:\mathrm{chord}\:\mathrm{cut} \\ $$$$\mathrm{off}\:\mathrm{by}\:\mathrm{y}\:=\:\mathrm{2x}+\mathrm{1}\:\mathrm{from}\:\mathrm{circle}\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} =\mathrm{2} \\ $$
Answered by john santu last updated on 11/Jun/20
Commented by john santu last updated on 11/Jun/20
![A^⌢ B^⌢ = ∫_(−1) ^(0.2) (√(1+((dy/dx))^2 )) dx ⇔(d/dx) [ x^2 +y^2 = 2 ] 2x + 2yy ′ = 0 ; y′ = −(x/y) (y′)^2 = (x^2 /(2−x^2 )) . A^⌢ B^⌢ = ∫_(−1) ^(0.2) (√(1+(x^2 /(2−x^2 )))) dx = ∫_(−1) ^(0.2) (√(2/(2−x^2 ))) dx = (√2) ∫_(−1) ^(0.2) (dx/( (√(2−x^2 )))) set x = (√2) sin t [ ∫ (((√2) cos t dt)/( (√(2(1−sin^2 t))))) = sin^(−1) ((x/( (√2)))) ] then A^⌢ B^⌢ = (√2) [ sin^(−1) ((x/( (√2)))) ]_(−1) ^(0.2) = (√2) (sin^(−1) ((1/(5(√2))))+(π/4) )](https://www.tinkutara.com/question/Q98103.png)
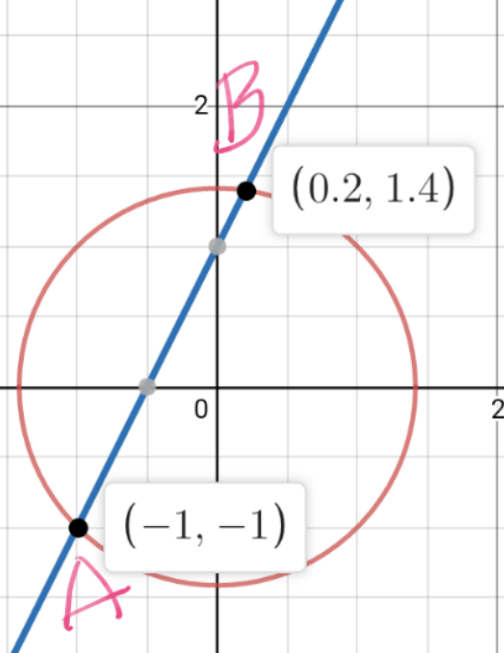
$$\overset{\frown} {\mathrm{A}}\overset{\frown} {\mathrm{B}}\:=\:\underset{−\mathrm{1}} {\overset{\mathrm{0}.\mathrm{2}} {\int}}\:\sqrt{\mathrm{1}+\left(\frac{\mathrm{dy}}{\mathrm{dx}}\right)^{\mathrm{2}} }\:\mathrm{dx}\: \\ $$$$\Leftrightarrow\frac{\mathrm{d}}{\mathrm{dx}}\:\left[\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \:=\:\mathrm{2}\:\right] \\ $$$$\mathrm{2x}\:+\:\mathrm{2yy}\:'\:=\:\mathrm{0}\:;\:\mathrm{y}'\:=\:−\frac{\mathrm{x}}{\mathrm{y}} \\ $$$$\left(\mathrm{y}'\right)^{\mathrm{2}} \:=\:\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}−\mathrm{x}^{\mathrm{2}} }\:. \\ $$$$\overset{\frown} {\mathrm{A}}\overset{\frown} {\mathrm{B}}\:=\:\underset{−\mathrm{1}} {\overset{\mathrm{0}.\mathrm{2}} {\int}}\:\sqrt{\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}−\mathrm{x}^{\mathrm{2}} }}\:\mathrm{dx}\: \\ $$$$=\:\underset{−\mathrm{1}} {\overset{\mathrm{0}.\mathrm{2}} {\int}}\:\sqrt{\frac{\mathrm{2}}{\mathrm{2}−\mathrm{x}^{\mathrm{2}} }}\:\mathrm{dx}\:=\:\sqrt{\mathrm{2}}\:\underset{−\mathrm{1}} {\overset{\mathrm{0}.\mathrm{2}} {\int}}\:\frac{\mathrm{dx}}{\:\sqrt{\mathrm{2}−\mathrm{x}^{\mathrm{2}} }} \\ $$$$\mathrm{set}\:\mathrm{x}\:=\:\sqrt{\mathrm{2}}\:\mathrm{sin}\:\mathrm{t}\: \\ $$$$\left[\:\int\:\frac{\sqrt{\mathrm{2}}\:\mathrm{cos}\:\mathrm{t}\:\mathrm{dt}}{\:\sqrt{\mathrm{2}\left(\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \mathrm{t}\right)}}\:=\:\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\:\sqrt{\mathrm{2}}}\right)\:\right] \\ $$$$\mathrm{then}\:\overset{\frown} {\mathrm{A}}\overset{\frown} {\mathrm{B}}\:=\:\sqrt{\mathrm{2}}\:\left[\:\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\:\sqrt{\mathrm{2}}}\right)\:\right]_{−\mathrm{1}} ^{\mathrm{0}.\mathrm{2}} \\ $$$$=\:\sqrt{\mathrm{2}}\:\left(\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{5}\sqrt{\mathrm{2}}}\right)+\frac{\pi}{\mathrm{4}}\:\right) \\ $$
Answered by mr W last updated on 11/Jun/20
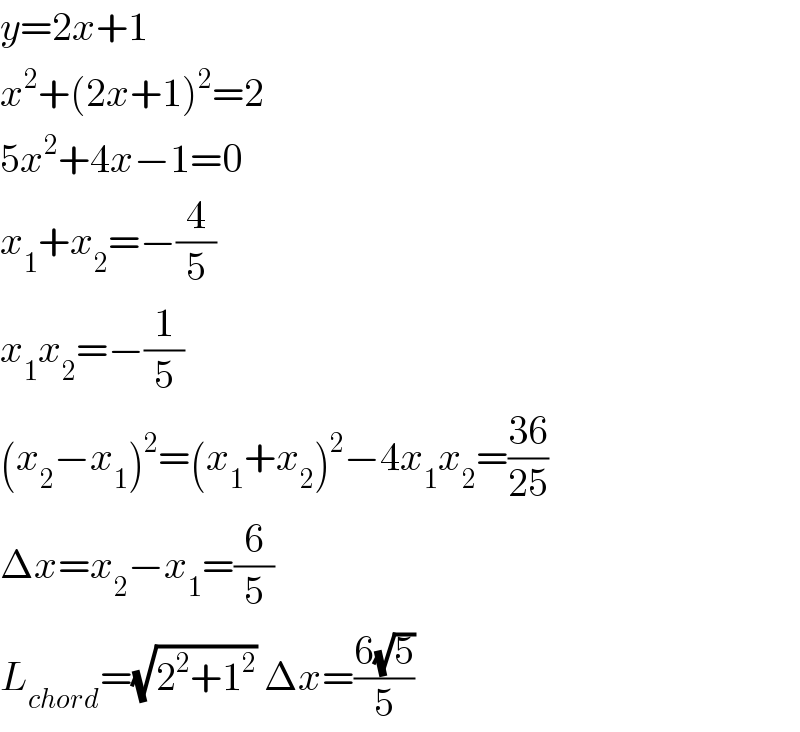
$${y}=\mathrm{2}{x}+\mathrm{1} \\ $$$${x}^{\mathrm{2}} +\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{2} \\ $$$$\mathrm{5}{x}^{\mathrm{2}} +\mathrm{4}{x}−\mathrm{1}=\mathrm{0} \\ $$$${x}_{\mathrm{1}} +{x}_{\mathrm{2}} =−\frac{\mathrm{4}}{\mathrm{5}} \\ $$$${x}_{\mathrm{1}} {x}_{\mathrm{2}} =−\frac{\mathrm{1}}{\mathrm{5}} \\ $$$$\left({x}_{\mathrm{2}} −{x}_{\mathrm{1}} \right)^{\mathrm{2}} =\left({x}_{\mathrm{1}} +{x}_{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{4}{x}_{\mathrm{1}} {x}_{\mathrm{2}} =\frac{\mathrm{36}}{\mathrm{25}} \\ $$$$\Delta{x}={x}_{\mathrm{2}} −{x}_{\mathrm{1}} =\frac{\mathrm{6}}{\mathrm{5}} \\ $$$${L}_{{chord}} =\sqrt{\mathrm{2}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} }\:\Delta{x}=\frac{\mathrm{6}\sqrt{\mathrm{5}}}{\mathrm{5}} \\ $$
Commented by bobhans last updated on 11/Jun/20

$$\mathrm{thank}\:\mathrm{you} \\ $$
Answered by 1549442205 last updated on 11/Jun/20

$$\mathrm{Intersection}\:\mathrm{points}\:\mathrm{of}\:\mathrm{the}\:\mathrm{line}\:\mathrm{y}=\mathrm{2x}+\mathrm{1}\:\mathrm{and}\: \\ $$$$\mathrm{the}\:\mathrm{circle}\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} =\mathrm{2}\:\mathrm{have}\:\mathrm{the}\:\mathrm{cordinates} \\ $$$$\mathrm{be}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{the}\:\mathrm{system}\:\mathrm{of}\:\mathrm{equations}: \\ $$$$\begin{cases}{\mathrm{y}=\mathrm{2x}+\mathrm{1}\left(\mathrm{1}\right)}\\{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} =\mathrm{2}\left(\mathrm{2}\right)}\end{cases} \\ $$$$\mathrm{Replace}\:\left(\mathrm{1}\right)\mathrm{into}\:\left(\mathrm{2}\right)\:\mathrm{we}\:\mathrm{get}\:\mathrm{x}^{\mathrm{2}} +\left(\mathrm{2x}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{2} \\ $$$$\Leftrightarrow\mathrm{5x}^{\mathrm{2}} +\mathrm{4x}−\mathrm{1}=\mathrm{0}\Leftrightarrow\mathrm{x}_{\mathrm{A}} =−\mathrm{1},\mathrm{x}_{\mathrm{B}} =\frac{\mathrm{1}}{\mathrm{5}}\Rightarrow\mathrm{y}_{\mathrm{A}} =−\mathrm{1},\mathrm{y}_{\mathrm{B}} =\frac{\mathrm{7}}{\mathrm{5}}.\mathrm{We}\:\mathrm{get} \\ $$$$\mathrm{A}\left(−\mathrm{1};−\mathrm{1}\right),\mathrm{B}\left(\frac{\mathrm{1}}{\mathrm{5}};\frac{\mathrm{7}}{\mathrm{5}}\right) \\ $$$$\mathrm{AB}=\sqrt{\left(\mathrm{x}_{\mathrm{A}} −\mathrm{x}_{\mathrm{B}} \right)^{\mathrm{2}} +\left(\mathrm{y}_{\mathrm{A}} −\mathrm{y}_{\mathrm{B}} \right)^{\mathrm{2}} }\: \\ $$$$=\sqrt{\left(\frac{\mathrm{6}}{\mathrm{5}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{12}}{\mathrm{5}}\right)^{\mathrm{2}} }\:=\sqrt{\frac{\mathrm{36}+\mathrm{144}}{\mathrm{25}}\:}\:=\sqrt{\frac{\mathrm{180}}{\mathrm{25}}}\:=\frac{\mathrm{6}\sqrt{\mathrm{5}}}{\mathrm{5}} \\ $$$$\mathrm{Thus},\mathrm{the}\:\mathrm{length}\:\mathrm{of}\:\mathrm{the}\:\mathrm{chord}\:\mathrm{AB}\:\mathrm{is}\:\frac{\mathrm{6}\sqrt{\mathrm{5}}}{\mathrm{5}} \\ $$
