Question Number 109955 by toa last updated on 26/Aug/20
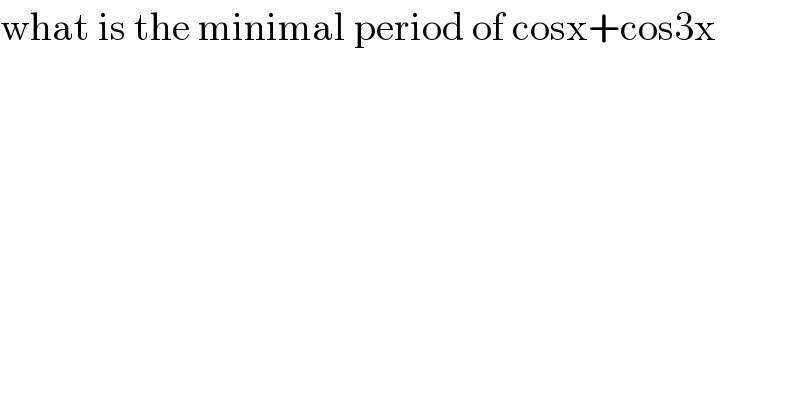
$$\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{minimal}\:\mathrm{period}\:\mathrm{of}\:\mathrm{cosx}+\mathrm{cos3x} \\ $$
Answered by mathmax by abdo last updated on 26/Aug/20

$$\mathrm{2}\pi \\ $$
Commented by toa last updated on 26/Aug/20
I know 2pi is the period, but can you explain better how it is the minimal period?
Answered by mathmax by abdo last updated on 26/Aug/20
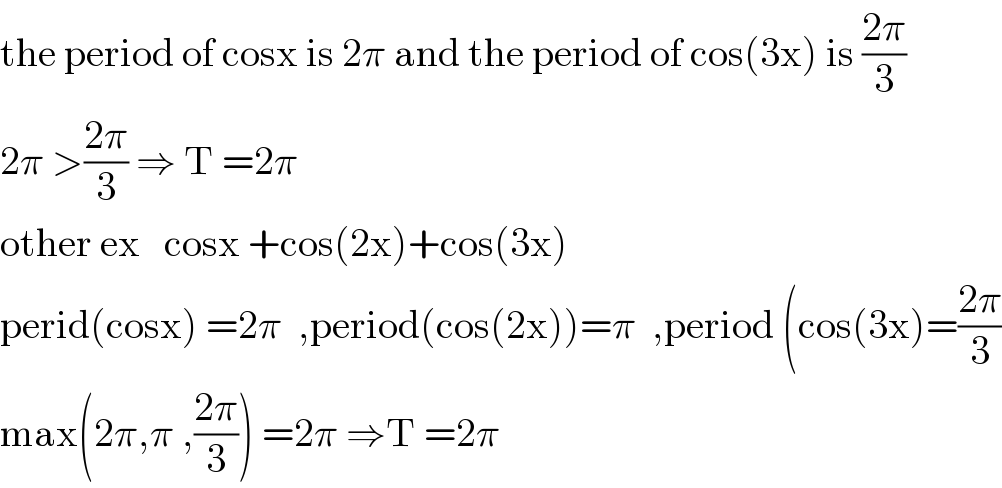
$$\mathrm{the}\:\mathrm{period}\:\mathrm{of}\:\mathrm{cosx}\:\mathrm{is}\:\mathrm{2}\pi\:\mathrm{and}\:\mathrm{the}\:\mathrm{period}\:\mathrm{of}\:\mathrm{cos}\left(\mathrm{3x}\right)\:\mathrm{is}\:\frac{\mathrm{2}\pi}{\mathrm{3}} \\ $$$$\mathrm{2}\pi\:>\frac{\mathrm{2}\pi}{\mathrm{3}}\:\Rightarrow\:\mathrm{T}\:=\mathrm{2}\pi\:\: \\ $$$$\mathrm{other}\:\mathrm{ex}\:\:\:\mathrm{cosx}\:+\mathrm{cos}\left(\mathrm{2x}\right)+\mathrm{cos}\left(\mathrm{3x}\right) \\ $$$$\mathrm{perid}\left(\mathrm{cosx}\right)\:=\mathrm{2}\pi\:\:,\mathrm{period}\left(\mathrm{cos}\left(\mathrm{2x}\right)\right)=\pi\:\:,\mathrm{period}\:\left(\mathrm{cos}\left(\mathrm{3x}\right)=\frac{\mathrm{2}\pi}{\mathrm{3}}\right. \\ $$$$\mathrm{max}\left(\mathrm{2}\pi,\pi\:,\frac{\mathrm{2}\pi}{\mathrm{3}}\right)\:=\mathrm{2}\pi\:\Rightarrow\mathrm{T}\:=\mathrm{2}\pi \\ $$
Answered by PRITHWISH SEN 2 last updated on 26/Aug/20
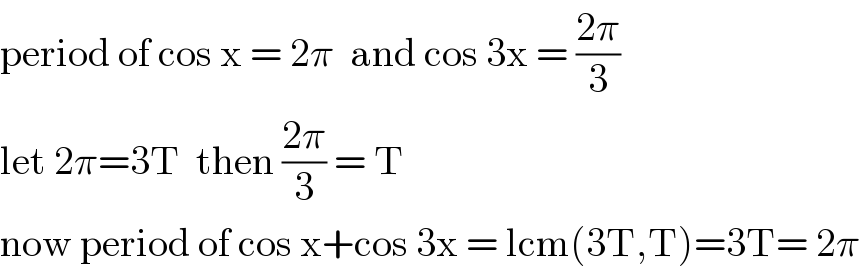
$$\mathrm{period}\:\mathrm{of}\:\mathrm{cos}\:\mathrm{x}\:=\:\mathrm{2}\pi\:\:\mathrm{and}\:\mathrm{cos}\:\mathrm{3x}\:=\:\frac{\mathrm{2}\pi}{\mathrm{3}} \\ $$$$\mathrm{let}\:\mathrm{2}\pi=\mathrm{3T}\:\:\mathrm{then}\:\frac{\mathrm{2}\pi}{\mathrm{3}}\:=\:\mathrm{T} \\ $$$$\mathrm{now}\:\mathrm{period}\:\mathrm{of}\:\mathrm{cos}\:\mathrm{x}+\mathrm{cos}\:\mathrm{3x}\:=\:\mathrm{lcm}\left(\mathrm{3T},\mathrm{T}\right)=\mathrm{3T}=\:\mathrm{2}\pi \\ $$
