Menu Close

what-is-the-number-positive-integral-solutions-for-xy-72-x-y-

Tinku Tara 0 Comments
Pin




Question Number 106409 by bemath last updated on 05/Aug/20
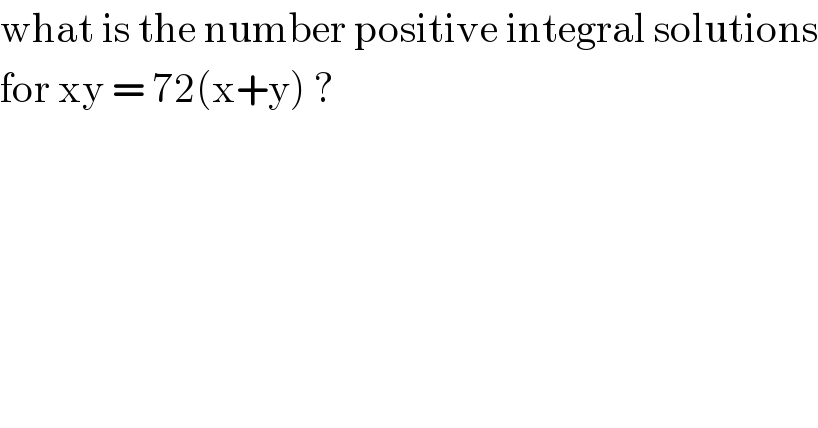
what is the number positive integral solutions for xy = 72(x+y) ?
$$\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{number}\:\mathrm{positive}\:\mathrm{integral}\:\mathrm{solutions} \\ $$$$\mathrm{for}\:\mathrm{xy}\:=\:\mathrm{72}\left(\mathrm{x}+\mathrm{y}\right)\:? \\ $$
Answered by 1549442205PVT last updated on 05/Aug/20
We have xy=72(x+y)⇔(x−72)(y−72)=72^2 (∗) =(8.9)^2 =2^6 .3^4 .Hence (x−72)∣(2^6 .3^4 ) Since (2^6 .3^4 )has (6+1)(4+1)=35 positive divisors,the given equation has 35 poitive integer solutions Note 35 positive divisors of 72^2 =2^6 .3^4 are:{1,2,3,4,6, 8, 9, 12, 16, 18, 24, 27,32 48, 36,54, 64, 72, 81, 96, 108, 144, 162, 192,216,288 ,324,432, 576, 648, 864, 1296,1728,2592 ,5184}
$$\mathrm{We}\:\mathrm{have}\: \\ $$$$\mathrm{xy}=\mathrm{72}\left(\mathrm{x}+\mathrm{y}\right)\Leftrightarrow\left(\mathrm{x}−\mathrm{72}\right)\left(\mathrm{y}−\mathrm{72}\right)=\mathrm{72}^{\mathrm{2}} \:\left(\ast\right) \\ $$$$=\left(\mathrm{8}.\mathrm{9}\right)^{\mathrm{2}} =\mathrm{2}^{\mathrm{6}} .\mathrm{3}^{\mathrm{4}} .\mathrm{Hence}\:\left(\mathrm{x}−\mathrm{72}\right)\mid\left(\mathrm{2}^{\mathrm{6}} .\mathrm{3}^{\mathrm{4}} \right) \\ $$$$\mathrm{Since}\:\left(\mathrm{2}^{\mathrm{6}} .\mathrm{3}^{\mathrm{4}} \right)\mathrm{has}\:\left(\mathrm{6}+\mathrm{1}\right)\left(\mathrm{4}+\mathrm{1}\right)=\mathrm{35}\:\mathrm{positive} \\ $$$$\mathrm{divisors},\mathrm{the}\:\mathrm{given}\:\mathrm{equation}\:\mathrm{has}\:\mathrm{35} \\ $$$$\mathrm{poitive}\:\mathrm{integer}\:\mathrm{solutions} \\ $$$$\mathrm{Note}\:\mathrm{35}\:\mathrm{positive}\:\mathrm{divisors}\:\mathrm{of}\:\mathrm{72}^{\mathrm{2}} =\mathrm{2}^{\mathrm{6}} .\mathrm{3}^{\mathrm{4}} \\ $$$$\boldsymbol{\mathrm{are}}:\left\{\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4},\mathrm{6},\:\mathrm{8},\:\mathrm{9},\:\mathrm{12},\:\mathrm{16},\:\mathrm{18},\:\mathrm{24},\:\mathrm{27},\mathrm{32}\:\right. \\ $$$$\mathrm{48},\:\mathrm{36},\mathrm{54},\:\mathrm{64},\:\mathrm{72},\:\mathrm{81},\:\mathrm{96},\:\mathrm{108},\:\mathrm{144},\:\mathrm{162}, \\ $$$$\mathrm{192},\mathrm{216},\mathrm{288}\:,\mathrm{324},\mathrm{432},\:\mathrm{576},\:\mathrm{648},\:\mathrm{864}, \\ $$$$\left.\mathrm{1296},\mathrm{1728},\mathrm{2592}\:,\mathrm{5184}\right\} \\ $$
Commented by Rasheed.Sindhi last updated on 05/Aug/20
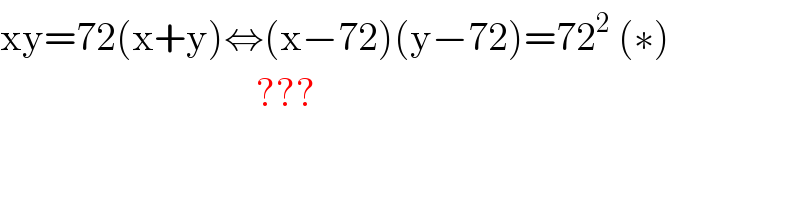
xy=72(x+y)⇔(x−72)(y−72)=72^2 (∗) ???
$$\mathrm{xy}=\mathrm{72}\left(\mathrm{x}+\mathrm{y}\right)\Leftrightarrow\left(\mathrm{x}−\mathrm{72}\right)\left(\mathrm{y}−\mathrm{72}\right)=\mathrm{72}^{\mathrm{2}} \:\left(\ast\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:??? \\ $$
Commented by bemath last updated on 05/Aug/20
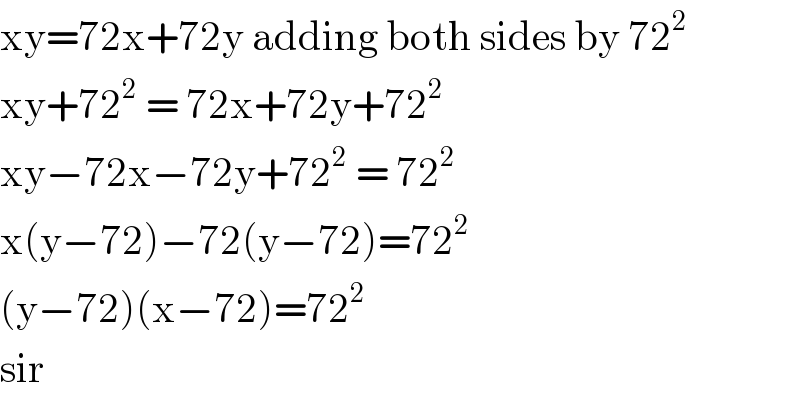
xy=72x+72y adding both sides by 72^2 xy+72^2 = 72x+72y+72^2 xy−72x−72y+72^2 = 72^2 x(y−72)−72(y−72)=72^2 (y−72)(x−72)=72^2 sir
$$\mathrm{xy}=\mathrm{72x}+\mathrm{72y}\:\mathrm{adding}\:\mathrm{both}\:\mathrm{sides}\:\mathrm{by}\:\mathrm{72}^{\mathrm{2}} \\ $$$$\mathrm{xy}+\mathrm{72}^{\mathrm{2}} \:=\:\mathrm{72x}+\mathrm{72y}+\mathrm{72}^{\mathrm{2}} \\ $$$$\mathrm{xy}−\mathrm{72x}−\mathrm{72y}+\mathrm{72}^{\mathrm{2}} \:=\:\mathrm{72}^{\mathrm{2}} \\ $$$$\mathrm{x}\left(\mathrm{y}−\mathrm{72}\right)−\mathrm{72}\left(\mathrm{y}−\mathrm{72}\right)=\mathrm{72}^{\mathrm{2}} \\ $$$$\left(\mathrm{y}−\mathrm{72}\right)\left(\mathrm{x}−\mathrm{72}\right)=\mathrm{72}^{\mathrm{2}} \: \\ $$$$\mathrm{sir}\: \\ $$
Commented by Rasheed.Sindhi last updated on 05/Aug/20
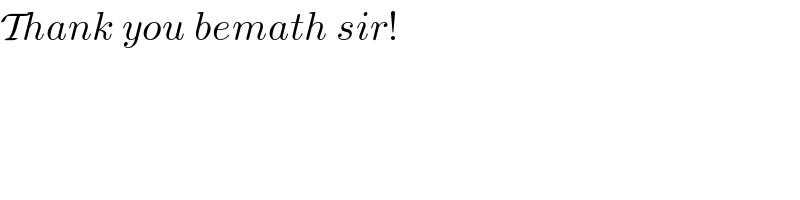
Thank you bemath sir!
$$\mathcal{T}{hank}\:{you}\:{bemath}\:{sir}! \\ $$
Commented by Rasheed.Sindhi last updated on 05/Aug/20
V. Nice sir 1549...
$${V}.\:{Nice}\:{sir}\:\mathrm{1549}… \\ $$
Answered by Rasheed.Sindhi last updated on 05/Aug/20
Wrong Approach Solved for integral solutions._(−) ^★ As the expression is symmetric so if (a,b) satisfy, (b,a) also satisfy. xy=72(x+y)⇒ x×(y/(x+y))=72 (x & (y/(x+y)) are divisors of 72 and product of both is 72) determinant ((x,(y/(x+y)),(=(y/(x+y))),),(1,( 72),(=(y/(1+y))),(y=((−72)/(71))∉Z)),(2,( 36),(=(y/(2+y))),(y=((−72)/(35))∉Z)),(3,( 24),(=(y/(3+y))),(y=((−72)/(23))∉Z)),(4,( 18),(=(y/(4+y))),(y=((−72)/(17))∉Z)),(6,( 12),(=(y/(6+y))),(y=((−72)/(11))∉Z)),(8,( 9),(=(y/(8+y))),(y=((−72)/8)=−9)),(9,( 8),(=(y/(9+y))),(y=((−72)/7)∉Z)),((12),( 6),(=(y/(12+y))),(y=((−72)/5)∉Z)),((18),( 4),(=(y/(18+y))),(y=((−72)/3)=−24)),((24),( 3),(=(y/(24+y))),(y=((−72)/2)=−36)),((36),( 2),(=(y/(36+y))),(y=((−72)/1)=−72)),((72),( 1),(=(y/(72+y))),(y=No value))) (8,−9),(−9,8),(18,−24),(−24,18) (24,−36),(−36,24),(36,−72),(−72,36) 8 integral solutions Ans: No positive integral solution.
$${Wrong}\:{Approach} \\ $$$$\underset{−} {{Solved}\:{for}\:\boldsymbol{{integral}}\:\boldsymbol{{solutions}}.} \\ $$$$\:^{\bigstar} {As}\:{the}\:{expression}\:{is}\:{symmetric} \\ $$$${so}\:{if}\:\left({a},{b}\right)\:{satisfy},\:\left({b},{a}\right)\:{also}\:{satisfy}. \\ $$$${xy}=\mathrm{72}\left({x}+{y}\right)\Rightarrow \\ $$$${x}×\frac{{y}}{{x}+{y}}=\mathrm{72} \\ $$$$\left({x}\:\&\:\frac{{y}}{{x}+{y}}\:{are}\:{divisors}\:{of}\:\mathrm{72}\:{and}\right. \\ $$$$\left.{product}\:{of}\:{both}\:{is}\:\mathrm{72}\right) \\ $$$$\begin{vmatrix}{{x}}&{\frac{{y}}{{x}+{y}}}&{=\frac{{y}}{{x}+{y}}}&{}\\{\mathrm{1}}&{\:\:\mathrm{72}}&{=\frac{{y}}{\mathrm{1}+{y}}}&{{y}=\frac{−\mathrm{72}}{\mathrm{71}}\notin\mathbb{Z}}\\{\mathrm{2}}&{\:\:\:\mathrm{36}}&{=\frac{{y}}{\mathrm{2}+{y}}}&{{y}=\frac{−\mathrm{72}}{\mathrm{35}}\notin\mathbb{Z}}\\{\mathrm{3}}&{\:\:\:\mathrm{24}}&{=\frac{{y}}{\mathrm{3}+{y}}}&{{y}=\frac{−\mathrm{72}}{\mathrm{23}}\notin\mathbb{Z}}\\{\mathrm{4}}&{\:\:\mathrm{18}}&{=\frac{{y}}{\mathrm{4}+{y}}}&{{y}=\frac{−\mathrm{72}}{\mathrm{17}}\notin\mathbb{Z}}\\{\mathrm{6}}&{\:\:\:\mathrm{12}}&{=\frac{{y}}{\mathrm{6}+{y}}}&{{y}=\frac{−\mathrm{72}}{\mathrm{11}}\notin\mathbb{Z}}\\{\mathrm{8}}&{\:\:\:\:\:\mathrm{9}}&{=\frac{{y}}{\mathrm{8}+{y}}}&{{y}=\frac{−\mathrm{72}}{\mathrm{8}}=−\mathrm{9}}\\{\mathrm{9}}&{\:\:\:\:\:\mathrm{8}}&{=\frac{{y}}{\mathrm{9}+{y}}}&{{y}=\frac{−\mathrm{72}}{\mathrm{7}}\notin\mathbb{Z}}\\{\mathrm{12}}&{\:\:\:\:\:\mathrm{6}}&{=\frac{{y}}{\mathrm{12}+{y}}}&{{y}=\frac{−\mathrm{72}}{\mathrm{5}}\notin\mathbb{Z}}\\{\mathrm{18}}&{\:\:\:\:\:\mathrm{4}}&{=\frac{{y}}{\mathrm{18}+{y}}}&{{y}=\frac{−\mathrm{72}}{\mathrm{3}}=−\mathrm{24}}\\{\mathrm{24}}&{\:\:\:\:\:\mathrm{3}}&{=\frac{{y}}{\mathrm{24}+{y}}}&{{y}=\frac{−\mathrm{72}}{\mathrm{2}}=−\mathrm{36}}\\{\mathrm{36}}&{\:\:\:\:\:\mathrm{2}}&{=\frac{{y}}{\mathrm{36}+{y}}}&{{y}=\frac{−\mathrm{72}}{\mathrm{1}}=−\mathrm{72}}\\{\mathrm{72}}&{\:\:\:\:\:\mathrm{1}}&{=\frac{{y}}{\mathrm{72}+{y}}}&{{y}={No}\:{value}}\end{vmatrix} \\ $$$$\left(\mathrm{8},−\mathrm{9}\right),\left(−\mathrm{9},\mathrm{8}\right),\left(\mathrm{18},−\mathrm{24}\right),\left(−\mathrm{24},\mathrm{18}\right) \\ $$$$\left(\mathrm{24},−\mathrm{36}\right),\left(−\mathrm{36},\mathrm{24}\right),\left(\mathrm{36},−\mathrm{72}\right),\left(−\mathrm{72},\mathrm{36}\right) \\ $$$$\mathrm{8}\:{integral}\:{solutions} \\ $$$${Ans}: \\ $$$${No}\:{positive}\:{integral}\:{solution}. \\ $$
Commented by Her_Majesty last updated on 05/Aug/20
you are wrong xy=72(x+y) ⇒ y=((72x)/(x−72)) if we look for x≤y and x, y>0 ⇒ 72<x≤144 x∈{73, 74, 75, 76, 78, 80, 81, 84, 88, 90, 96, 99, 104, 108, 120, 126, 136, 144} ⇒ 35 solutions y=((72x)/(x−72)) x=72+n y=((72(n+72))/n) ⇒ n∣72∨n∣(n+72)
$${you}\:{are}\:{wrong} \\ $$$${xy}=\mathrm{72}\left({x}+{y}\right)\:\Rightarrow\:{y}=\frac{\mathrm{72}{x}}{{x}−\mathrm{72}} \\ $$$${if}\:{we}\:{look}\:{for}\:{x}\leqslant{y}\:{and}\:{x},\:{y}>\mathrm{0}\:\Rightarrow\:\mathrm{72}<{x}\leqslant\mathrm{144} \\ $$$${x}\in\left\{\mathrm{73},\:\mathrm{74},\:\mathrm{75},\:\mathrm{76},\:\mathrm{78},\:\mathrm{80},\:\mathrm{81},\:\mathrm{84},\:\mathrm{88},\:\mathrm{90},\:\mathrm{96},\:\mathrm{99},\:\mathrm{104},\:\mathrm{108},\:\mathrm{120},\:\mathrm{126},\:\mathrm{136},\:\mathrm{144}\right\} \\ $$$$\Rightarrow\:\mathrm{35}\:{solutions} \\ $$$$ \\ $$$${y}=\frac{\mathrm{72}{x}}{{x}−\mathrm{72}} \\ $$$${x}=\mathrm{72}+{n} \\ $$$${y}=\frac{\mathrm{72}\left({n}+\mathrm{72}\right)}{{n}}\:\Rightarrow\:{n}\mid\mathrm{72}\vee{n}\mid\left({n}+\mathrm{72}\right) \\ $$
Commented by Rasheed.Sindhi last updated on 05/Aug/20
Thanks madam! Now I recognized my logical error. The answer is not editable but it′s completely discardable!
$$\mathcal{T}{hanks}\:{madam}!\:{Now}\:{I} \\ $$$${recognized}\:{my}\:\boldsymbol{{logical}}\:\boldsymbol{{error}}. \\ $$$${The}\:{answer}\:{is}\:{not}\:{editable}\:{but} \\ $$$${it}'{s}\:{completely}\:{discardable}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *