What-is-the-number-value-of-f-log-x-1-x-1-1-3-x-x-for-f-1-a-0-1-b-27-c-81-d-10-e-12-

Question Number 114597 by O Predador last updated on 19/Sep/20

What is the number value of f [\sqrt[3]{\log (\frac{\sqrt{x} - 1}{x - 1})}] = \sqrt{\sqrt{x} + x} for f (- 1) ?

a) 0, 1

b) 27

c) 81

d) 10

e) 12

Answered by Olaf last updated on 19/Sep/20

\sqrt[3]{\log (\frac{\sqrt{x} - 1}{x - 1})} = - 1

\log (\frac{\sqrt{x} - 1}{x - 1}) = - 1

\frac{\sqrt{x} - 1}{x - 1} = 10^{- 1} = \frac{1}{10}

\sqrt{x} - 1 = \frac{1}{10} (x - 1)

x - 10 \sqrt{x} + 9 = 0

(\sqrt{x} - 1) (\sqrt{x} - 9) = 0

\sqrt{x} = 1 : impossible

otherwise \frac{\sqrt{x} - 1}{x - 1} is not defined

\sqrt{x} = 9 \Rightarrow \sqrt{\sqrt{x} + x} = \sqrt{90} = 3 \sqrt{10}

Sorry but I find 3 \sqrt{10}

I supposed \log is \log_{10} and not \ln

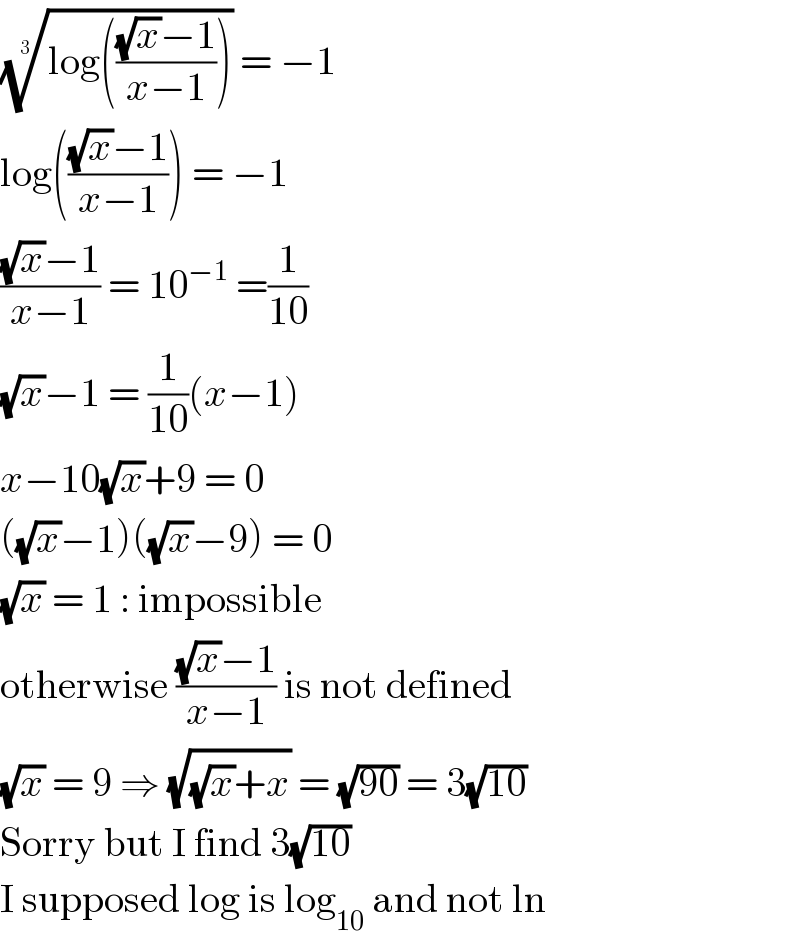
Commented by O Predador last updated on 20/Sep/20

Thank you!

Answered by floor(10²Eta[1]) last updated on 20/Sep/20

f (\sqrt[3]{\log (\frac{\sqrt{x} - 1}{x - 1})}) = \sqrt{\sqrt{x} + x}

\sqrt[3]{\log (\frac{\sqrt{x} - 1}{x - 1})} = - 1 \Rightarrow \log (\frac{\sqrt{x} - 1}{x - 1}) = - 1

\frac{\sqrt{x} - 1}{x - 1} = 10^{- 1} = \frac{1}{10} \Rightarrow 10 \sqrt{x} - 10 = x - 1

10 \sqrt{x} = x + 9

100 x = x^{2} + 18 x + 81

x^{2} - 82 x + 81 = 0

x = \frac{82 \pm 80}{2} \Rightarrow x = 1 or 81 \Rightarrow x = 81 (because x \neq 1)

x = 81 \Rightarrow

f (- 1) = \sqrt{\sqrt{81} + 81} = \sqrt{90}

now if \log is \ln the logic is the same and

the answer is \sqrt{e^{2} - e}

Answered by 1549442205PVT last updated on 20/Sep/20

We need find x > 0, x \neq 1 such that

\log \frac{\sqrt{x} - 1}{x - 1} = - 1 \Leftrightarrow \log \frac{\sqrt{x} - 1}{(\sqrt{x} - 1) (\sqrt{x} + 1)} = - 1

\Leftrightarrow \log \frac{1}{\sqrt{x} + 1} = - 1 \Leftrightarrow - \log (\sqrt{x} + 1) = - 1

∙ If logx = \log_{10} x then

\Leftrightarrow \log (\sqrt{x} + 1) = 1 \Rightarrow \sqrt{x} + 1 = 10

\Leftrightarrow \sqrt{x} = 9 \Leftrightarrow x = 81

\Rightarrow f (- 1) = \sqrt{9 + 81} = \sqrt{90}

∙ If logx = lnx then \sqrt{x} + 1 = e \Rightarrow \sqrt{x} = e - 1

\Rightarrow x = e^{2} - 2 e + 1 \Rightarrow f (- 1) = \sqrt{e^{2} - e}

Available answer is false!