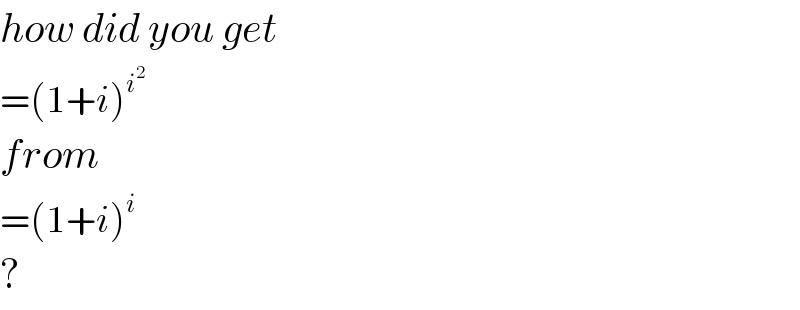What-is-the-real-part-and-imaginary-part-of-the-complex-number-z-1-i-i-

Question Number 25152 by tawa tawa last updated on 05/Dec/17

What is the real part and imaginary part of the complex number : z = {(1 + i)}^{i}

Commented by tawa tawa last updated on 05/Dec/17

please help .

Answered by jota+ last updated on 05/Dec/17

z = {(1 + i)}^{i}

l n z = i l n (1 + i) = i [l n (\sqrt{2} e^{i π / 4})]

= i [l n \sqrt{2} + i \frac{π}{4}] = (- \frac{π}{4} + i l n \sqrt{2})

z = e^{- π / 4} e^{i l n \sqrt{2}} =

= e^{- π / 4} [c o s (l n \sqrt{2}) + i s i n (l n \sqrt{2})]

Commented by mrW1 last updated on 05/Dec/17

v e r y n i c e!

Commented by ajfour last updated on 05/Dec/17

i n d e e d!

Commented by tawa tawa last updated on 05/Dec/17

God bless you sir .

Answered by nnnavendu last updated on 05/Dec/17

Z = {(1 + i)}^{i}

= {(1 + i)}^{i} \times 1^{i} ∵ 1^{i} = 1

= {(1 + i)}^{i^{2}} ∵ i^{2} = - 1

= {(1 + i)}^{- 1}

= \frac{1}{(1 + i)}

= \frac{1}{(1 + i)} \times \frac{(1 - i)}{(1 - i)}

= \frac{(1 - i)}{(1^{2} - i^{2})} ∵ i^{2} = - 1

= \frac{1 - i}{1 + 1}

= \frac{1 - i}{2}

= \frac{1}{2} - \frac{i}{2}

r e a l p a r t \frac{1}{2}, i m a g i n a r y p a r t \frac{- i}{2}

Commented by mrW1 last updated on 05/Dec/17

h o w d i d y o u g e t

= {(1 + i)}^{i^{2}}

f r o m

= {(1 + i)}^{i}

?

Facebook Tweet Pin