Menu Close

what-is-the-remainder-when-111-222-333-77-is-divided-by-37-

Tinku Tara 0 Comments
Pin




Question Number 34044 by NECx last updated on 29/Apr/18
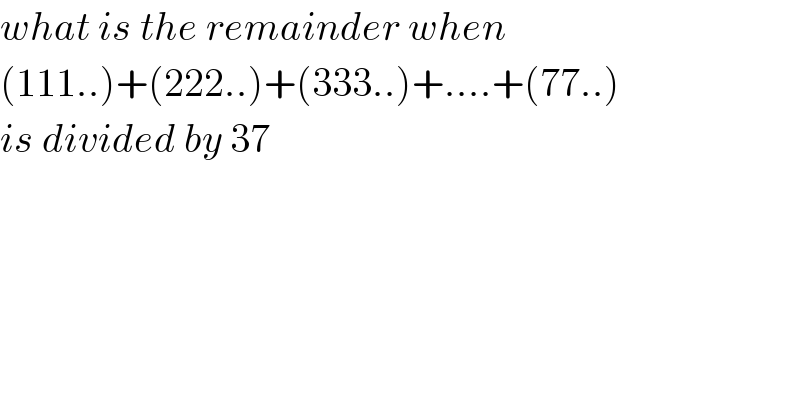
what is the remainder when (111..)+(222..)+(333..)+....+(77..) is divided by 37
$${what}\:{is}\:{the}\:{remainder}\:{when}\: \\ $$$$\left(\mathrm{111}..\right)+\left(\mathrm{222}..\right)+\left(\mathrm{333}..\right)+….+\left(\mathrm{77}..\right) \\ $$$${is}\:{divided}\:{by}\:\mathrm{37} \\ $$
Commented by Rasheed.Sindhi last updated on 30/Apr/18
N=(111..)+(222..)+(333..)+....+(77..) =1(111...)+2(111..)+3(111...)...+7(111..) =(1+2+3+...+7)(11...) =28×111... Let 111...is of n-digits number. For n=1 N=28.1=28, If 28 is divided by 37 the remainder is 28 ....... .... If n=3k,the remainder is 0 If n=3k+1,the remainder is 28 If n=3k+2,the remainder is 12 The remainders : 0,28,12
$$\mathrm{N}=\left(\mathrm{111}..\right)+\left(\mathrm{222}..\right)+\left(\mathrm{333}..\right)+….+\left(\mathrm{77}..\right) \\ $$$$ \\ $$$$=\mathrm{1}\left(\mathrm{111}…\right)+\mathrm{2}\left(\mathrm{111}..\right)+\mathrm{3}\left(\mathrm{111}…\right)…+\mathrm{7}\left(\mathrm{111}..\right) \\ $$$$=\left(\mathrm{1}+\mathrm{2}+\mathrm{3}+…+\mathrm{7}\right)\left(\mathrm{11}…\right) \\ $$$$=\mathrm{28}×\mathrm{111}… \\ $$$$\mathrm{Let}\:\mathrm{111}…\mathrm{is}\:\mathrm{of}\:\mathrm{n}-\mathrm{digits}\:\mathrm{number}. \\ $$$$\mathrm{For}\:\mathrm{n}=\mathrm{1} \\ $$$$\mathrm{N}=\mathrm{28}.\mathrm{1}=\mathrm{28},\: \\ $$$$\mathrm{If}\:\mathrm{28}\:\mathrm{is}\:\mathrm{divided}\:\mathrm{by}\:\mathrm{37}\:\mathrm{the}\:\mathrm{remainder}\:\mathrm{is}\:\mathrm{28} \\ $$$$……. \\ $$$$…. \\ $$$$\mathrm{If}\:\mathrm{n}=\mathrm{3k},\mathrm{the}\:\mathrm{remainder}\:\mathrm{is}\:\:\mathrm{0} \\ $$$$\mathrm{If}\:\mathrm{n}=\mathrm{3k}+\mathrm{1},\mathrm{the}\:\mathrm{remainder}\:\mathrm{is}\:\mathrm{28} \\ $$$$\mathrm{If}\:\mathrm{n}=\mathrm{3k}+\mathrm{2},\mathrm{the}\:\mathrm{remainder}\:\mathrm{is}\:\mathrm{12} \\ $$$$\mathrm{The}\:\mathrm{remainders}\::\:\mathrm{0},\mathrm{28},\mathrm{12} \\ $$
Commented by NECx last updated on 30/Apr/18
thank you so much buddy
$${thank}\:{you}\:{so}\:{much}\:{buddy} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 30/Apr/18
(111...)+(222...)+(333...)+....+(777...) (111...)+2(111...)+3(111...)+...+7(111...) let value of (111...) say=t t(1+2+3+...+7) t(28) now let us find the value of (111...upto n ) then put n→∞ (111...upto n terms) 1+10+10^2 +10^3 +.... (((10^n −1))/(10−1)) 28t (37−9)t (37−9)(((10^n −1))/9) ((37)/9)(10^n −1)+(1−10^n ) when devided by 37 first part is divisble by 37 remaining is remainder under the condktion n→∞ pls recheck the question pls
$$\left(\mathrm{111}…\right)+\left(\mathrm{222}…\right)+\left(\mathrm{333}…\right)+….+\left(\mathrm{777}…\right) \\ $$$$\left(\mathrm{111}…\right)+\mathrm{2}\left(\mathrm{111}…\right)+\mathrm{3}\left(\mathrm{111}…\right)+…+\mathrm{7}\left(\mathrm{111}…\right) \\ $$$${let}\:{value}\:{of}\:\left(\mathrm{111}…\right)\:{say}={t} \\ $$$${t}\left(\mathrm{1}+\mathrm{2}+\mathrm{3}+…+\mathrm{7}\right) \\ $$$${t}\left(\mathrm{28}\right) \\ $$$${now}\:{let}\:{us}\:{find}\:{the}\:{value}\:{of}\:\left(\mathrm{111}…{upto}\:{n}\:\right)\:{then} \\ $$$${put}\:{n}\rightarrow\infty \\ $$$$\left(\mathrm{111}…{upto}\:{n}\:{terms}\right) \\ $$$$\mathrm{1}+\mathrm{10}+\mathrm{10}^{\mathrm{2}} +\mathrm{10}^{\mathrm{3}} +…. \\ $$$$\frac{\left(\mathrm{10}^{{n}} −\mathrm{1}\right)}{\mathrm{10}−\mathrm{1}} \\ $$$$\mathrm{28}{t} \\ $$$$\left(\mathrm{37}−\mathrm{9}\right){t} \\ $$$$\left(\mathrm{37}−\mathrm{9}\right)\frac{\left(\mathrm{10}^{{n}} −\mathrm{1}\right)}{\mathrm{9}} \\ $$$$\frac{\mathrm{37}}{\mathrm{9}}\left(\mathrm{10}^{{n}} −\mathrm{1}\right)+\left(\mathrm{1}−\mathrm{10}^{{n}} \right) \\ $$$${when}\:{devided}\:{by}\:\mathrm{37}\:{first}\:{part}\:{is}\:{divisble}\:{by}\:\mathrm{37} \\ $$$${remaining}\:{is}\:{remainder}\:{under}\:{the}\:{condktion}\:{n}\rightarrow\infty \\ $$$${pls}\:{recheck}\:{the}\:{question}\:{pls} \\ $$$$ \\ $$
Commented by NECx last updated on 30/Apr/18
wow.... lemme check it..Really I love what you just did.Thanks
$${wow}….\:{lemme}\:{check}\:{it}..{Really} \\ $$$${I}\:{love}\:{what}\:{you}\:{just}\:{did}.{Thanks} \\ $$
Commented by Rasheed.Sindhi last updated on 30/Apr/18
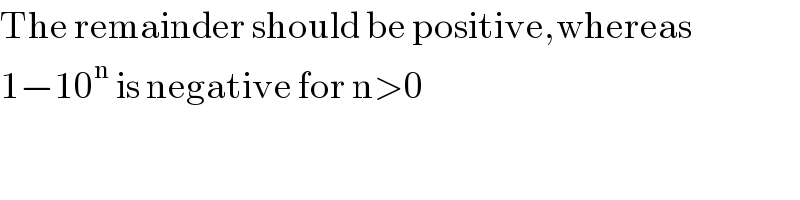
The remainder should be positive,whereas 1−10^n is negative for n>0
$$\mathrm{The}\:\mathrm{remainder}\:\mathrm{should}\:\mathrm{be}\:\mathrm{positive},\mathrm{whereas} \\ $$$$\mathrm{1}−\mathrm{10}^{\mathrm{n}} \:\mathrm{is}\:\mathrm{negative}\:\mathrm{for}\:\mathrm{n}>\mathrm{0} \\ $$
Answered by 5a3k last updated on 30/Apr/18
[(111..)+(222..)+(333..)+...+(777..)] ((37[3+6+9+...+21])/(37)) 3+6+9+....+21 7/2[2×3+(7−1)3] 84
$$\left[\left(\mathrm{111}..\right)+\left(\mathrm{222}..\right)+\left(\mathrm{333}..\right)+…+\left(\mathrm{777}..\right)\right] \\ $$$$\frac{\mathrm{37}\left[\mathrm{3}+\mathrm{6}+\mathrm{9}+…+\mathrm{21}\right]}{\mathrm{37}} \\ $$$$\mathrm{3}+\mathrm{6}+\mathrm{9}+….+\mathrm{21} \\ $$$$\mathrm{7}/\mathrm{2}\left[\mathrm{2}×\mathrm{3}+\left(\mathrm{7}−\mathrm{1}\right)\mathrm{3}\right] \\ $$$$\mathrm{84} \\ $$
Commented by NECx last updated on 30/Apr/18
not clear please
$${not}\:{clear}\:{please} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *