Question Number 34139 by NECx last updated on 01/May/18
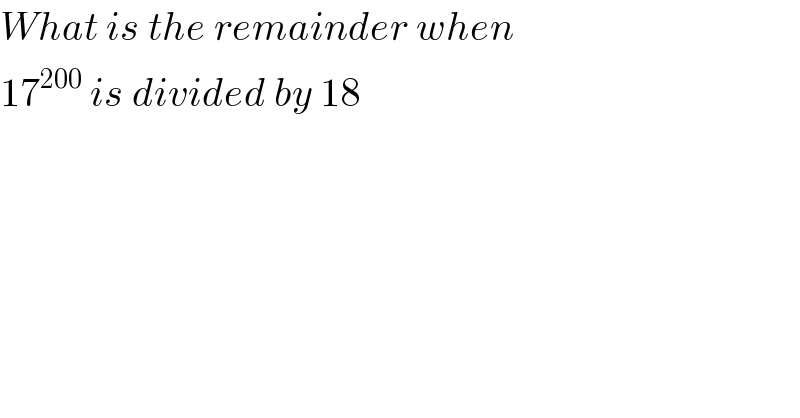
$${What}\:{is}\:{the}\:{remainder}\:{when} \\ $$$$\mathrm{17}^{\mathrm{200}} \:{is}\:{divided}\:{by}\:\mathrm{18} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 01/May/18
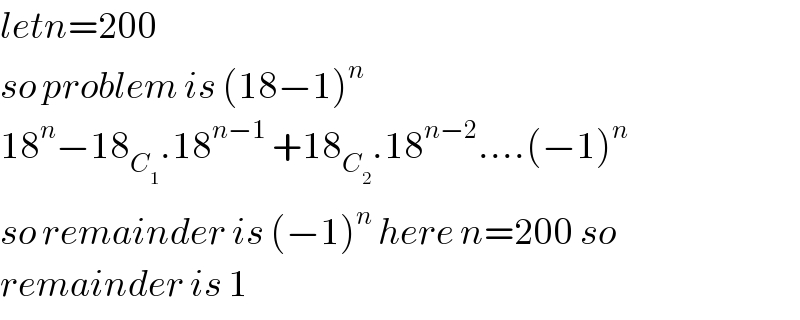
$${letn}=\mathrm{200} \\ $$$${so}\:{problem}\:{is}\:\left(\mathrm{18}−\mathrm{1}\right)^{{n}} \\ $$$$\mathrm{18}^{{n}} −\mathrm{18}_{{C}_{\mathrm{1}} } .\mathrm{18}^{{n}−\mathrm{1}} \:+\mathrm{18}_{{C}_{\mathrm{2}} } .\mathrm{18}^{{n}−\mathrm{2}} ….\left(−\mathrm{1}\right)^{{n}} \\ $$$${so}\:{remainder}\:{is}\:\left(−\mathrm{1}\right)^{{n}} \:{here}\:{n}=\mathrm{200}\:{so}\: \\ $$$${remainder}\:{is}\:\mathrm{1} \\ $$
Answered by Rasheed.Sindhi last updated on 04/May/18

$$\mathrm{17}\equiv−\mathrm{1}\left(\mathrm{mod}\:\mathrm{18}\right) \\ $$$$\left(\mathrm{17}\right)^{\mathrm{200}} \equiv\left(−\mathrm{1}\right)^{\mathrm{200}} =\mathrm{1}\left(\mathrm{mod}\:\mathrm{18}\right) \\ $$$$\left(\mathrm{17}\right)^{\mathrm{200}} \equiv\mathrm{1}\left(\mathrm{mod}\:\mathrm{18}\right) \\ $$
Commented by Rasheed.Sindhi last updated on 09/May/18
$$\mathrm{Mr}\:\mathrm{NECx}\:\mathrm{pl}\:\mathrm{confirm}\:\mathrm{the}\:\mathrm{answer}. \\ $$
