Menu Close

What-is-the-shortest-distance-between-two-parabolas-y-2-x-2-and-x-2-y-2-

Tinku Tara 0 Comments
Pin




Question Number 123243 by benjo_mathlover last updated on 24/Nov/20
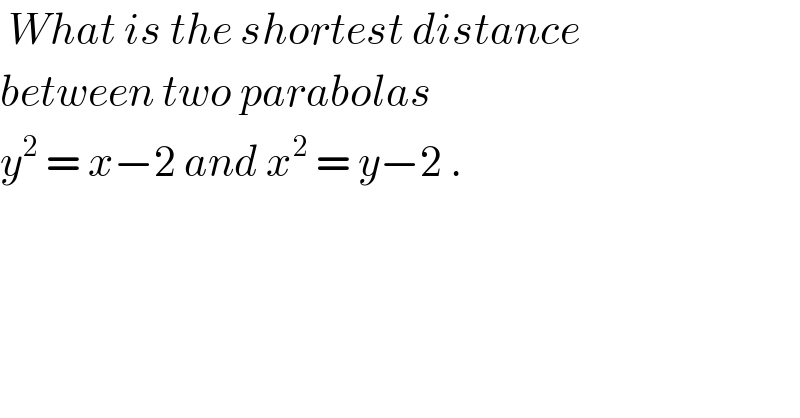
What is the shortest distance between two parabolas y^2 = x−2 and x^2 = y−2 .
$$\:{What}\:{is}\:{the}\:{shortest}\:{distance} \\ $$$${between}\:{two}\:{parabolas}\: \\ $$$${y}^{\mathrm{2}} \:=\:{x}−\mathrm{2}\:{and}\:{x}^{\mathrm{2}} \:=\:{y}−\mathrm{2}\:. \\ $$
Commented by liberty last updated on 24/Nov/20
In other way by normal line of two parabolas :y=x^2 +2 { ((grad normal = −(1/(2x)))),((point P(a,a^2 +2))) :} :y^2 =x−2 { ((grad normal =−2y)),((point Q(b^2 +2,b) )) :} { ((equation of normal ⇒y_1 =−(1/(2a))x+a^2 +2)),((equation of normal ⇒y_2 =−2bx+2b^3 +5b)) :} these are the same line . { ((−(1/(2a)) = −2b ; a=(1/(4b)))),((a^2 +2 = 2b^3 +5b ; 64b^5 +160b^3 −80b^2 −2=0)) :} The only real number answer is b=(1/2) and a=(1/2) so the two points on the parabolas are { ((P((1/2),(9/4)))),((Q((9/4),(1/2)))) :} The distance = (√(2×((9/4)−(2/4))^2 )) = (7/4)(√2)
$${In}\:{other}\:{way}\:{by}\:{normal}\:{line}\:{of}\:{two} \\ $$$${parabolas}\::{y}={x}^{\mathrm{2}} +\mathrm{2\begin{cases}{{grad}\:{normal}\:=\:−\frac{\mathrm{1}}{\mathrm{2}{x}}}\\{{point}\:{P}\left({a},{a}^{\mathrm{2}} +\mathrm{2}\right)}\end{cases}} \\ $$$$:{y}^{\mathrm{2}} \:={x}−\mathrm{2}\:\begin{cases}{{grad}\:{normal}\:=−\mathrm{2}{y}}\\{{point}\:{Q}\left({b}^{\mathrm{2}} +\mathrm{2},{b}\right)\:}\end{cases} \\ $$$$\begin{cases}{{equation}\:{of}\:{normal}\:\Rightarrow{y}_{\mathrm{1}} =−\frac{\mathrm{1}}{\mathrm{2}{a}}{x}+{a}^{\mathrm{2}} +\mathrm{2}}\\{{equation}\:{of}\:{normal}\:\Rightarrow{y}_{\mathrm{2}} =−\mathrm{2}{bx}+\mathrm{2}{b}^{\mathrm{3}} +\mathrm{5}{b}}\end{cases} \\ $$$${these}\:{are}\:{the}\:{same}\:{line}\:. \\ $$$$\begin{cases}{−\frac{\mathrm{1}}{\mathrm{2}{a}}\:=\:−\mathrm{2}{b}\:;\:{a}=\frac{\mathrm{1}}{\mathrm{4}{b}}}\\{{a}^{\mathrm{2}} +\mathrm{2}\:=\:\mathrm{2}{b}^{\mathrm{3}} +\mathrm{5}{b}\:;\:\mathrm{64}{b}^{\mathrm{5}} +\mathrm{160}{b}^{\mathrm{3}} −\mathrm{80}{b}^{\mathrm{2}} −\mathrm{2}=\mathrm{0}}\end{cases} \\ $$$${The}\:{only}\:{real}\:{number}\:{answer}\:{is}\: \\ $$$${b}=\frac{\mathrm{1}}{\mathrm{2}}\:{and}\:{a}=\frac{\mathrm{1}}{\mathrm{2}}\:{so}\:{the}\:{two}\:{points} \\ $$$${on}\:{the}\:{parabolas}\:{are}\:\begin{cases}{{P}\left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{9}}{\mathrm{4}}\right)}\\{{Q}\left(\frac{\mathrm{9}}{\mathrm{4}},\frac{\mathrm{1}}{\mathrm{2}}\right)}\end{cases} \\ $$$${The}\:{distance}\:=\:\sqrt{\mathrm{2}×\left(\frac{\mathrm{9}}{\mathrm{4}}−\frac{\mathrm{2}}{\mathrm{4}}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{7}}{\mathrm{4}}\sqrt{\mathrm{2}}\: \\ $$$$ \\ $$$$ \\ $$
Commented by benjo_mathlover last updated on 24/Nov/20
Commented by benjo_mathlover last updated on 24/Nov/20
correct. thank you
$${correct}.\:{thank}\:{you} \\ $$
Answered by bobhans last updated on 24/Nov/20
(•) y^2 =x−2 (•) x^2 =y−2 2y.y′ = 1 2x = y′ grad y′=(1/(2y))=(1/(2a)) grad y′=2x=2b Point A(a^2 +2,a) Point B(b,b^2 +2) tangent line tangent line y=(1/(2a))(x−(a^2 +2))+a y=2b(x−b)+b^2 +2 two tangent line are parallel ⇒ (1/(2a)) = 2b ⇔ b = (1/(4a)) so the shortest distance is ∣AB∣ =(√((a^2 +2−b)^2 +(a−(b^2 +2))^2 )) =(√((a^2 +2−(1/(4a)))^2 +(a−(1/(16a^2 ))−2)^2 )) =(√((((4a^3 +8a−1)/(4a)))^2 +(((16a^3 −32a^2 −1)/(16a^2 )))^2 )) we compute ((d∣AB∣)/da) = 0 we get a=(1/2) ∧ b=(1/2) ∣AB∣_(min) = (√(((1/4)+2−(1/2))^2 +((1/2)−(1/4)−2)^2 )) = (√(2((9/4)−(2/4))^2 )) = ((7(√2))/4) .
$$\:\:\left(\bullet\right)\:{y}^{\mathrm{2}} ={x}−\mathrm{2}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\bullet\right)\:{x}^{\mathrm{2}} ={y}−\mathrm{2} \\ $$$$\:\:\mathrm{2}{y}.{y}'\:=\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}{x}\:=\:{y}' \\ $$$$\:{grad}\:{y}'=\frac{\mathrm{1}}{\mathrm{2}{y}}=\frac{\mathrm{1}}{\mathrm{2}{a}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{grad}\:{y}'=\mathrm{2}{x}=\mathrm{2}{b} \\ $$$$\:\:{Point}\:{A}\left({a}^{\mathrm{2}} +\mathrm{2},{a}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{Point}\:{B}\left({b},{b}^{\mathrm{2}} +\mathrm{2}\right) \\ $$$${tangent}\:{line}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{tangent}\:{line} \\ $$$${y}=\frac{\mathrm{1}}{\mathrm{2}{a}}\left({x}−\left({a}^{\mathrm{2}} +\mathrm{2}\right)\right)+{a}\:\:\:\:\:\:{y}=\mathrm{2}{b}\left({x}−{b}\right)+{b}^{\mathrm{2}} +\mathrm{2} \\ $$$${two}\:{tangent}\:{line}\:{are}\:{parallel} \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{\mathrm{2}{a}}\:=\:\mathrm{2}{b}\:\Leftrightarrow\:{b}\:=\:\frac{\mathrm{1}}{\mathrm{4}{a}} \\ $$$${so}\:{the}\:{shortest}\:{distance}\:{is} \\ $$$$\mid{AB}\mid\:=\sqrt{\left({a}^{\mathrm{2}} +\mathrm{2}−{b}\right)^{\mathrm{2}} +\left({a}−\left({b}^{\mathrm{2}} +\mathrm{2}\right)\right)^{\mathrm{2}} } \\ $$$$=\sqrt{\left({a}^{\mathrm{2}} +\mathrm{2}−\frac{\mathrm{1}}{\mathrm{4}{a}}\right)^{\mathrm{2}} +\left({a}−\frac{\mathrm{1}}{\mathrm{16}{a}^{\mathrm{2}} }−\mathrm{2}\right)^{\mathrm{2}} } \\ $$$$=\sqrt{\left(\frac{\mathrm{4}{a}^{\mathrm{3}} +\mathrm{8}{a}−\mathrm{1}}{\mathrm{4}{a}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{16}{a}^{\mathrm{3}} −\mathrm{32}{a}^{\mathrm{2}} −\mathrm{1}}{\mathrm{16}{a}^{\mathrm{2}} }\right)^{\mathrm{2}} } \\ $$$${we}\:{compute}\:\frac{{d}\mid{AB}\mid}{{da}}\:=\:\mathrm{0} \\ $$$${we}\:{get}\:{a}=\frac{\mathrm{1}}{\mathrm{2}}\:\wedge\:{b}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mid{AB}\mid_{{min}} \:=\:\sqrt{\left(\frac{\mathrm{1}}{\mathrm{4}}+\mathrm{2}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{2}\right)^{\mathrm{2}} } \\ $$$$\:=\:\sqrt{\mathrm{2}\left(\frac{\mathrm{9}}{\mathrm{4}}−\frac{\mathrm{2}}{\mathrm{4}}\right)^{\mathrm{2}} }\:=\:\frac{\mathrm{7}\sqrt{\mathrm{2}}}{\mathrm{4}}\:.\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *