Question Number 89776 by john santu last updated on 19/Apr/20
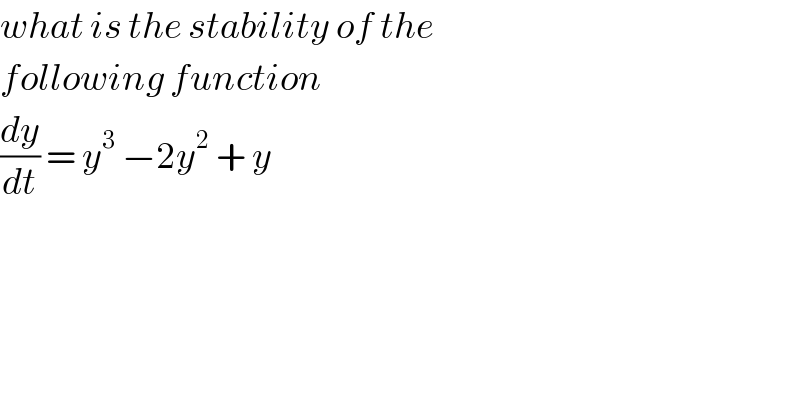
$${what}\:{is}\:{the}\:{stability}\:{of}\:{the}\: \\ $$$${following}\:{function}\: \\ $$$$\frac{{dy}}{{dt}}\:=\:{y}^{\mathrm{3}} \:−\mathrm{2}{y}^{\mathrm{2}} \:+\:{y}\: \\ $$
Commented by jagoll last updated on 19/Apr/20
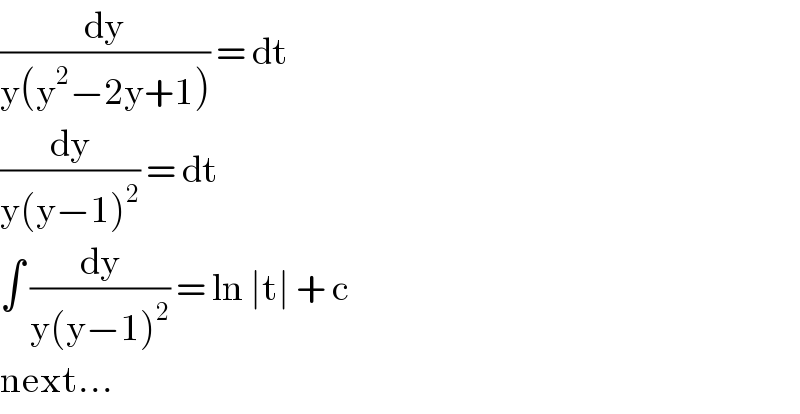
$$\frac{\mathrm{dy}}{\mathrm{y}\left(\mathrm{y}^{\mathrm{2}} −\mathrm{2y}+\mathrm{1}\right)}\:=\:\mathrm{dt} \\ $$$$\frac{\mathrm{dy}}{\mathrm{y}\left(\mathrm{y}−\mathrm{1}\right)^{\mathrm{2}} }\:=\:\mathrm{dt}\: \\ $$$$\int\:\frac{\mathrm{dy}}{\mathrm{y}\left(\mathrm{y}−\mathrm{1}\right)^{\mathrm{2}} }\:=\:\mathrm{ln}\:\mid\mathrm{t}\mid\:+\:\mathrm{c}\: \\ $$$$\mathrm{next}… \\ $$
Commented by john santu last updated on 19/Apr/20
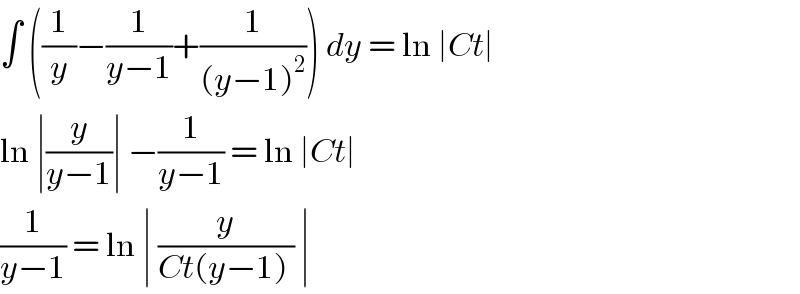
$$\int\:\left(\frac{\mathrm{1}}{{y}}−\frac{\mathrm{1}}{{y}−\mathrm{1}}+\frac{\mathrm{1}}{\left({y}−\mathrm{1}\right)^{\mathrm{2}} }\right)\:{dy}\:=\:\mathrm{ln}\:\mid{Ct}\mid\: \\ $$$$\mathrm{ln}\:\mid\frac{{y}}{{y}−\mathrm{1}}\mid\:−\frac{\mathrm{1}}{{y}−\mathrm{1}}\:=\:\mathrm{ln}\:\mid{Ct}\mid\: \\ $$$$\frac{\mathrm{1}}{{y}−\mathrm{1}}\:=\:\mathrm{ln}\:\mid\:\frac{{y}}{{Ct}\left({y}−\mathrm{1}\right)\:}\:\mid\: \\ $$
