what-is-the-sum-of-all-even-factors-of-1000-

Question Number 181275 by Linton last updated on 23/Nov/22

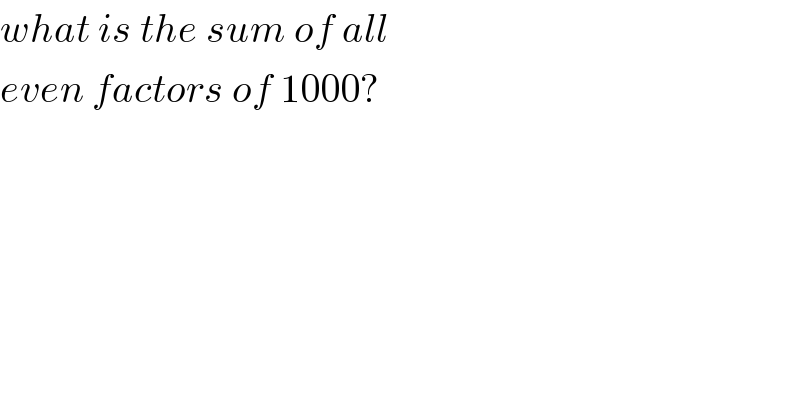
w h a t i s t h e s u m o f a l l

e v e n f a c t o r s o f 1000 ?

Commented by Rasheed.Sindhi last updated on 24/Nov/22

��

Commented by Linton last updated on 24/Nov/22

w e l l d o n e

Commented by Acem last updated on 24/Nov/22

♡ ♡

Commented by Frix last updated on 23/Nov/22

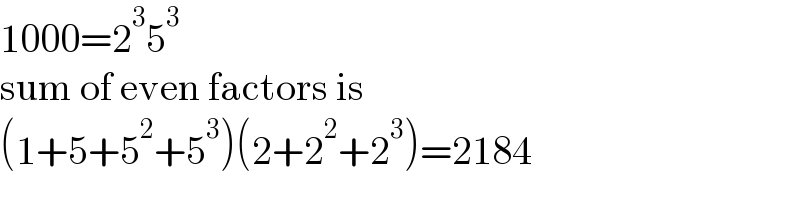
1000 = 2^{3} 5^{3}

sum of even factors is

(1 + 5 + 5^{2} + 5^{3}) (2 + 2^{2} + 2^{3}) = 2184

Commented by Rasheed.Sindhi last updated on 23/Nov/22

S i r t h i s i s a c o m p l e t e s o l u t i o n,

m o r e t h a n a c o m m e n t!

Commented by Frix last updated on 23/Nov/22

I^{'} ve been afraid others might claim it is

n o t a complete solution because I {didn}^{'} t

explain it \dots

Commented by Acem last updated on 23/Nov/22

@ S i r R a s h e e d, H a v e a g o o d e v e n i n g b r o .

Answered by Acem last updated on 23/Nov/22

e v e n \times o d d = e v e n

t h e 1000 = 2^{3} 5^{3}

2^{i} 5^{j} \forall i : 2^{i} i s e v e n, \forall j : 5^{j} i s o d d

T h e r e q u e s t i s t h e s u m o f t h e e v e n f a c t o r s o f 1000

S u m = \underset{i = 1}{\sum^{3}} 2^{i} \underset{j = 0}{\sum^{3}} 5^{j} t h a t m e a n s w e h a v e 12 n u m b e r s

S u m = 14 \times 156 = 2 184

{I t}^{'} s f u n n y a p p e a r i n g t h e q u e s t i o n 1 0 0 0

Commented by Rasheed.Sindhi last updated on 24/Nov/22

I s t h e f o l l o w i n g c o r r e c t ? :

S u m o f e v e n f a c t o r s o f 1000

= 2 \times S u m o f a l l f a c t o r s o f 500

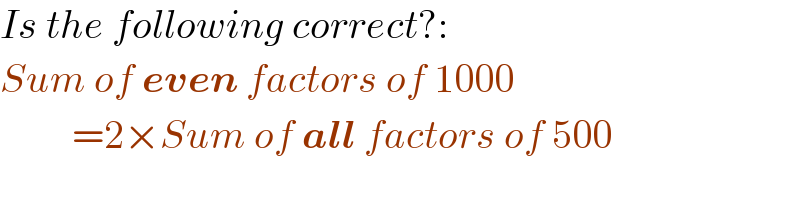
Commented by Linton last updated on 24/Nov/22

w e l l d o n e

Commented by Rasheed.Sindhi last updated on 24/Nov/22

@ A c e m, I a l s o t h i n k s o .

Commented by Acem last updated on 24/Nov/22

I t h i n k y e s, b e c a u s e e i t h e r i t f a c t o r s w e r e e v e n

o r o d d t h e r e s u l t a f t e r m u l t i p l y i n g t h e m b y 2

w i l l b e e v e n, r i g h t ?

Facebook Tweet Pin