What-is-the-sum-of-the-squares-of-the-roots-of-the-equation-x-2-7-x-5-0-Here-x-denotes-the-greatest-integer-less-than-or-equal-to-x-For-example-3-4-3-and-2-3-3-

Question Number 19409 by Tinkutara last updated on 10/Aug/17

What is the sum of the squares of the

roots of the equation x^{2} - 7 [x] + 5 = 0 ?

(Here [x] denotes the greatest integer

less than or equal to x . For example

[3.4] = 3 and [- 2.3] = - 3 .)

Commented by mrW1 last updated on 11/Aug/17

2 + 23 + 30 + 37 = 92

is this right ?

Answered by mrW1 last updated on 11/Aug/17

f (x) = x^{2} - 7 [x] + 5

let x = f + d with 0 ⩽ d < 1

\Rightarrow f (x) = {(f + d)}^{2} - 7 f + 5 = f^{2} + (2 d - 7) f + (d^{2} + 5)

f (x) ⩾ f^{2} - 7 f + 5 = g (x)

f (x) < f^{2} - 5 f + 6 = h (x)

g (x) = f^{2} - 7 f + 5 = (f - \frac{7 - \sqrt{29}}{2}) (f - \frac{7 + \sqrt{29}}{2})

h (x) = f^{2} - 5 f + 6 = (f - 2) (f - 3)

since g (x) ⩽ f (x) < h (x),

solution of f (x) = 0 :

\frac{7 - \sqrt{29}}{2} \approx 0.807 ⩽ f < 2 or

3 < f ⩽ \frac{7 + \sqrt{29}}{2} \approx 6.192

\Rightarrow f = 1, 4, 5, 6

with x = 1 + d :

{(1 + d)}^{2} - 7 \times 1 + 5 = 0

\Rightarrow d = \sqrt{2} - 1

\Rightarrow x = 1 + \sqrt{2} - 1 = \sqrt{2}

with x = 4 + d :

{(4 + d)}^{2} - 7 \times 4 + 5 = 0

\Rightarrow d = \sqrt{23} - 4

\Rightarrow x = 4 + \sqrt{23} - 4 = \sqrt{23}

with x = 5 + d :

{(5 + d)}^{2} - 7 \times 5 + 5 = 0

\Rightarrow d = \sqrt{30} - 5

\Rightarrow x = 5 + \sqrt{30} - 5 = \sqrt{30}

with x = 6 + d :

{(6 + d)}^{2} - 7 \times 6 + 5 = 0

\Rightarrow d = \sqrt{37} - 6

\Rightarrow x = 6 + \sqrt{37} - 6 = \sqrt{37}

all solutions :

\sqrt{2}, \sqrt{23}, \sqrt{30}, \sqrt{37}

sum of their squares :

2 + 23 + 30 + 37 = 92

Commented by mrW1 last updated on 11/Aug/17

Commented by Tinkutara last updated on 12/Aug/17

Thank you very much Sir! Awesome!

Answered by ajfour last updated on 12/Aug/17

let x = n + f

let x = [x] + {x} = n + f

then {(n + f)}^{2} + 5 - 7 n = 0

\Rightarrow {(n + f)}^{2} + 5 is an integer = 7 n

clearly 0 < n < 7 and 0 ⩽ f < 1

x = n + f = \sqrt{7 n - 5}, f = x - n

for n = 1, x = \sqrt{2}, f = \sqrt{2} - 1

n = 2, x = 3, f = 1

so not acceptable;

n = 3, x = 4, f = 1

not acceptable;

n = 4, x = \sqrt{23}, f = \sqrt{23} - 4

this is quite alright!

n = 5, x = \sqrt{30}, f = \sqrt{30} - 5

and if n = 6, x = \sqrt{37}, f = \sqrt{37} - 6

acceptable then are n = 1, 4, 5, 6

Σ x^{2} = Σ (7 n - 5)

= 2 + 23 + 30 + 37

= 92 .

Commented by ajfour last updated on 12/Aug/17

as {(n + f)}^{2} + 5 = 7 n

L . H . S . ⩾ 5 \Rightarrow 7 n ⩾ 5 so n > 0

for n > 7, n^{2} > 7 n

\Rightarrow {(n + f)}^{2} + 5 > 7 n

so n < 7 if {(n + f)}^{2} + 5 = 7 n .

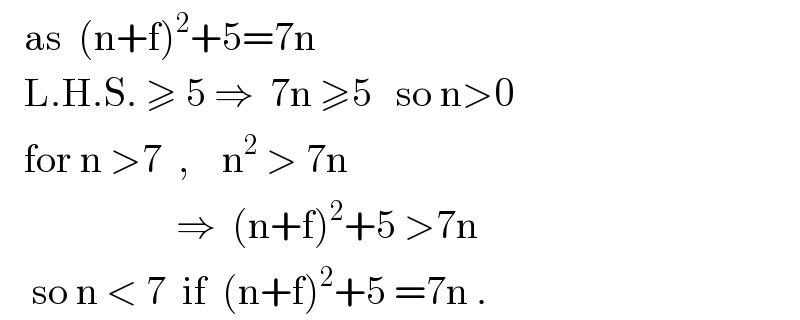
Commented by Tinkutara last updated on 12/Aug/17

Thank you very much Sir! Wonderful!

Commented by ajfour last updated on 12/Aug/17

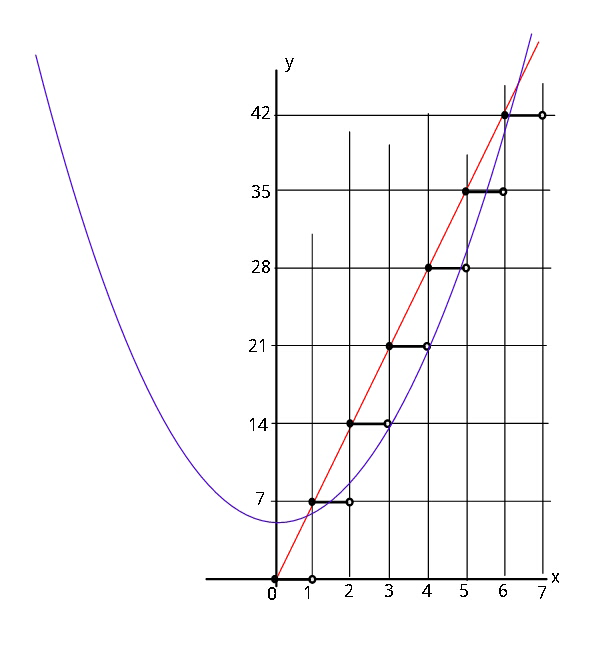
Commented by ajfour last updated on 12/Aug/17

y = 7 x; y = x^{2} + 5; y = 7 [x]

Facebook Tweet Pin