Menu Close

What-is-the-transformed-equation-of-a-parabola-given-by-y-2x-2-8-5-x-109-50-if-the-coordinate-axes-is-rotated-anticlockwise-by-tan-1-3-4-

Tinku Tara 0 Comments
Pin




Question Number 14664 by ajfour last updated on 03/Jun/17
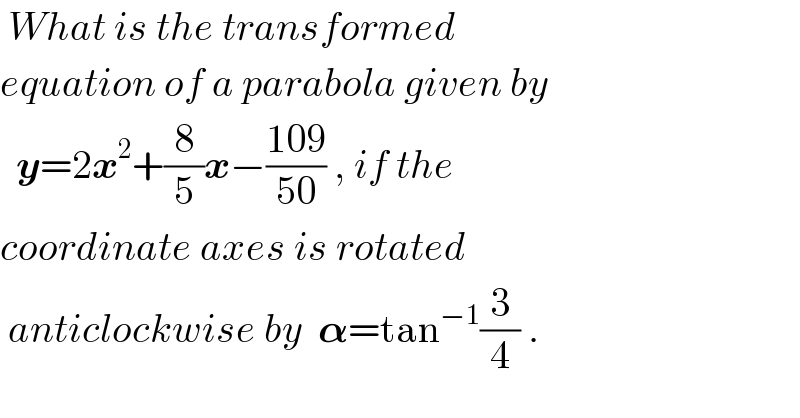
What is the transformed equation of a parabola given by y=2x^2 +(8/5)x−((109)/(50)) , if the coordinate axes is rotated anticlockwise by 𝛂=tan^(−1) (3/4) .
$$\:{What}\:{is}\:{the}\:{transformed}\: \\ $$$${equation}\:{of}\:{a}\:{parabola}\:{given}\:{by} \\ $$$$\:\:\boldsymbol{{y}}=\mathrm{2}\boldsymbol{{x}}^{\mathrm{2}} +\frac{\mathrm{8}}{\mathrm{5}}\boldsymbol{{x}}−\frac{\mathrm{109}}{\mathrm{50}}\:,\:{if}\:{the} \\ $$$${coordinate}\:{axes}\:{is}\:{rotated}\: \\ $$$$\:{anticlockwise}\:{by}\:\:\boldsymbol{\alpha}=\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{3}}{\mathrm{4}}\:. \\ $$
Answered by mrW1 last updated on 03/Jun/17
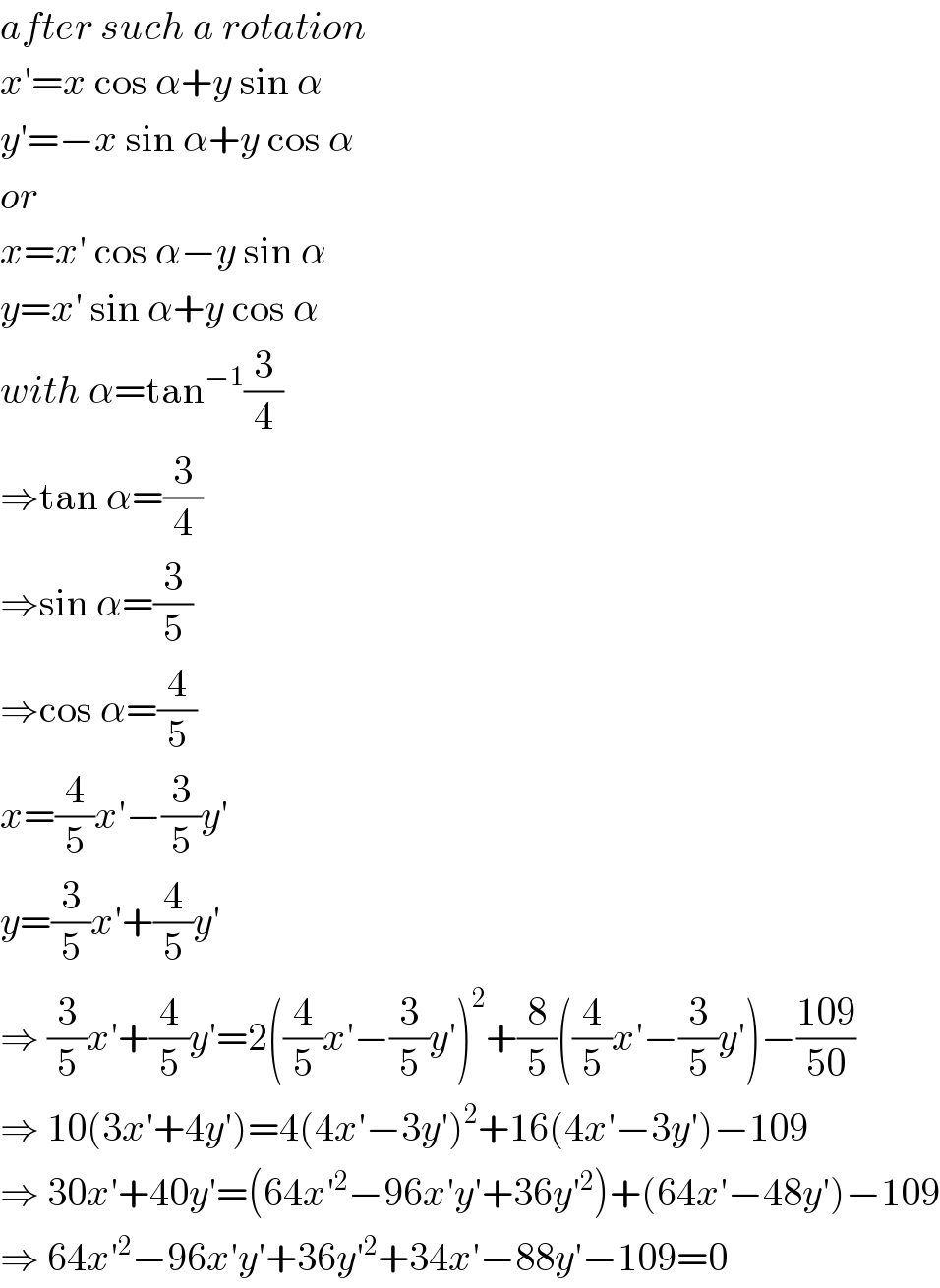
after such a rotation x′=x cos α+y sin α y′=−x sin α+y cos α or x=x′ cos α−y sin α y=x′ sin α+y cos α with α=tan^(−1) (3/4) ⇒tan α=(3/4) ⇒sin α=(3/5) ⇒cos α=(4/5) x=(4/5)x′−(3/5)y′ y=(3/5)x′+(4/5)y′ ⇒ (3/5)x′+(4/5)y′=2((4/5)x′−(3/5)y′)^2 +(8/5)((4/5)x′−(3/5)y′)−((109)/(50)) ⇒ 10(3x′+4y′)=4(4x′−3y′)^2 +16(4x′−3y′)−109 ⇒ 30x′+40y′=(64x′^2 −96x′y′+36y′^2 )+(64x′−48y′)−109 ⇒ 64x′^2 −96x′y′+36y′^2 +34x′−88y′−109=0
$${after}\:{such}\:{a}\:{rotation} \\ $$$${x}'={x}\:\mathrm{cos}\:\alpha+{y}\:\mathrm{sin}\:\alpha \\ $$$${y}'=−{x}\:\mathrm{sin}\:\alpha+{y}\:\mathrm{cos}\:\alpha \\ $$$${or} \\ $$$${x}={x}'\:\mathrm{cos}\:\alpha−{y}\:\mathrm{sin}\:\alpha \\ $$$${y}={x}'\:\mathrm{sin}\:\alpha+{y}\:\mathrm{cos}\:\alpha \\ $$$${with}\:\alpha=\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\Rightarrow\mathrm{tan}\:\alpha=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\Rightarrow\mathrm{sin}\:\alpha=\frac{\mathrm{3}}{\mathrm{5}} \\ $$$$\Rightarrow\mathrm{cos}\:\alpha=\frac{\mathrm{4}}{\mathrm{5}} \\ $$$${x}=\frac{\mathrm{4}}{\mathrm{5}}{x}'−\frac{\mathrm{3}}{\mathrm{5}}{y}' \\ $$$${y}=\frac{\mathrm{3}}{\mathrm{5}}{x}'+\frac{\mathrm{4}}{\mathrm{5}}{y}' \\ $$$$\Rightarrow\:\frac{\mathrm{3}}{\mathrm{5}}{x}'+\frac{\mathrm{4}}{\mathrm{5}}{y}'=\mathrm{2}\left(\frac{\mathrm{4}}{\mathrm{5}}{x}'−\frac{\mathrm{3}}{\mathrm{5}}{y}'\right)^{\mathrm{2}} +\frac{\mathrm{8}}{\mathrm{5}}\left(\frac{\mathrm{4}}{\mathrm{5}}{x}'−\frac{\mathrm{3}}{\mathrm{5}}{y}'\right)−\frac{\mathrm{109}}{\mathrm{50}} \\ $$$$\Rightarrow\:\mathrm{10}\left(\mathrm{3}{x}'+\mathrm{4}{y}'\right)=\mathrm{4}\left(\mathrm{4}{x}'−\mathrm{3}{y}'\right)^{\mathrm{2}} +\mathrm{16}\left(\mathrm{4}{x}'−\mathrm{3}{y}'\right)−\mathrm{109} \\ $$$$\Rightarrow\:\mathrm{30}{x}'+\mathrm{40}{y}'=\left(\mathrm{64}{x}'^{\mathrm{2}} −\mathrm{96}{x}'{y}'+\mathrm{36}{y}'^{\mathrm{2}} \right)+\left(\mathrm{64}{x}'−\mathrm{48}{y}'\right)−\mathrm{109} \\ $$$$\Rightarrow\:\mathrm{64}{x}'^{\mathrm{2}} −\mathrm{96}{x}'{y}'+\mathrm{36}{y}'^{\mathrm{2}} +\mathrm{34}{x}'−\mathrm{88}{y}'−\mathrm{109}=\mathrm{0} \\ $$
Commented by ajfour last updated on 03/Jun/17
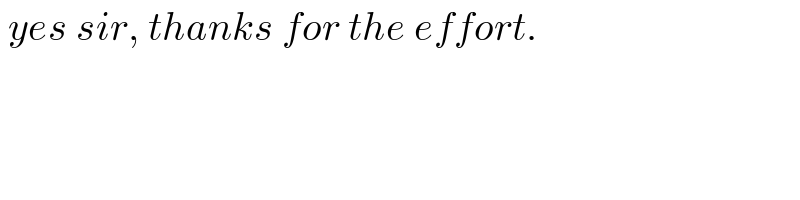
yes sir, thanks for the effort.
$$\:{yes}\:{sir},\:{thanks}\:{for}\:{the}\:{effort}. \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *