Question Number 173196 by AgniMath last updated on 08/Jul/22
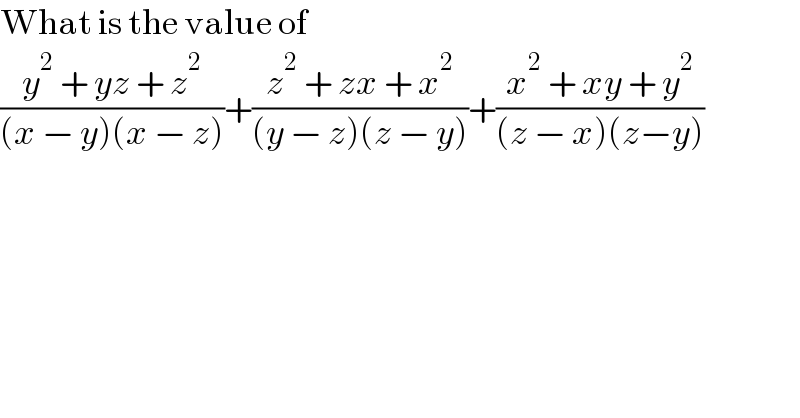
$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of} \\ $$$$\frac{{y}^{\mathrm{2}} \:+\:{yz}\:+\:{z}^{\mathrm{2}} }{\left({x}\:−\:{y}\right)\left({x}\:−\:{z}\right)}+\frac{{z}^{\mathrm{2}} \:+\:{zx}\:+\:{x}^{\mathrm{2}} }{\left({y}\:−\:{z}\right)\left({z}\:−\:{y}\right)}+\frac{{x}^{\mathrm{2}} \:+\:{xy}\:+\:{y}^{\mathrm{2}} }{\left({z}\:−\:{x}\right)\left({z}−{y}\right)} \\ $$
Commented by som(math1967) last updated on 08/Jul/22

$$\mathrm{0} \\ $$
Answered by Rasheed.Sindhi last updated on 08/Jul/22
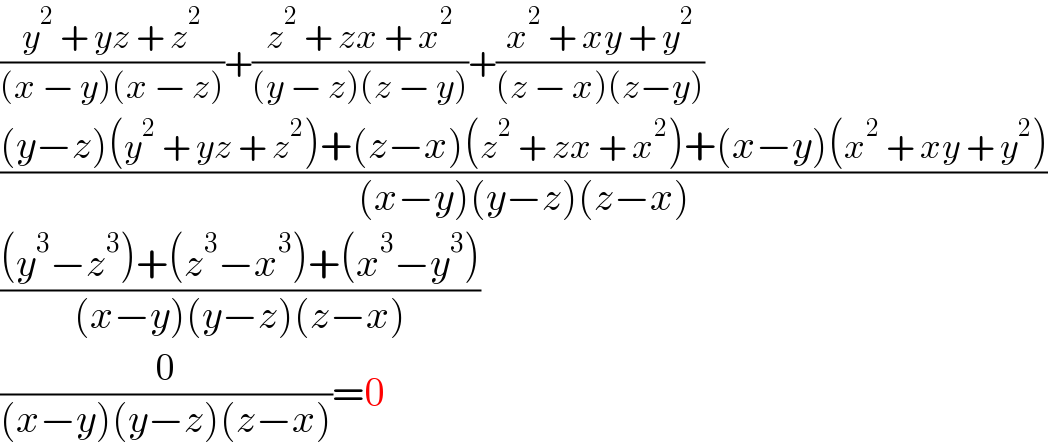
$$\frac{{y}^{\mathrm{2}} \:+\:{yz}\:+\:{z}^{\mathrm{2}} }{\left({x}\:−\:{y}\right)\left({x}\:−\:{z}\right)}+\frac{{z}^{\mathrm{2}} \:+\:{zx}\:+\:{x}^{\mathrm{2}} }{\left({y}\:−\:{z}\right)\left({z}\:−\:{y}\right)}+\frac{{x}^{\mathrm{2}} \:+\:{xy}\:+\:{y}^{\mathrm{2}} }{\left({z}\:−\:{x}\right)\left({z}−{y}\right)} \\ $$$$\frac{\left({y}−{z}\right)\left({y}^{\mathrm{2}} \:+\:{yz}\:+\:{z}^{\mathrm{2}} \right)+\left({z}−{x}\right)\left({z}^{\mathrm{2}} \:+\:{zx}\:+\:{x}^{\mathrm{2}} \right)+\left({x}−{y}\right)\left({x}^{\mathrm{2}} \:+\:{xy}\:+\:{y}^{\mathrm{2}} \right)}{\left({x}−{y}\right)\left({y}−{z}\right)\left({z}−{x}\right)} \\ $$$$\frac{\left({y}^{\mathrm{3}} −{z}^{\mathrm{3}} \right)+\left({z}^{\mathrm{3}} −{x}^{\mathrm{3}} \right)+\left({x}^{\mathrm{3}} −{y}^{\mathrm{3}} \right)}{\left({x}−{y}\right)\left({y}−{z}\right)\left({z}−{x}\right)} \\ $$$$\frac{\mathrm{0}}{\left({x}−{y}\right)\left({y}−{z}\right)\left({z}−{x}\right)}=\mathrm{0} \\ $$
