Question Number 116113 by Lordose last updated on 01/Oct/20
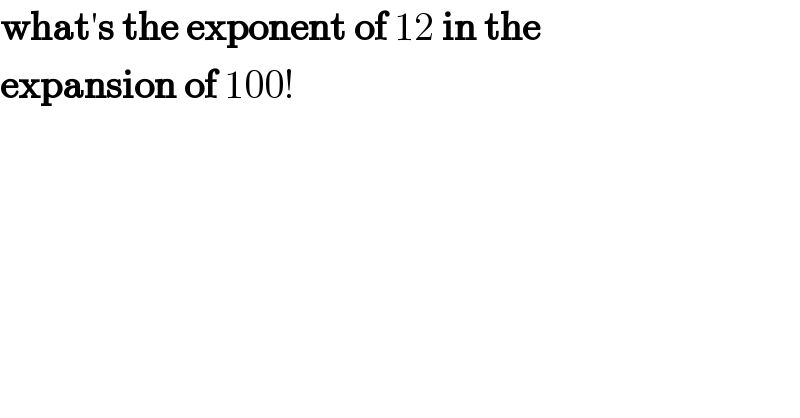
$$\boldsymbol{\mathrm{what}}'\boldsymbol{\mathrm{s}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{exponent}}\:\boldsymbol{\mathrm{of}}\:\mathrm{12}\:\boldsymbol{\mathrm{in}}\:\boldsymbol{\mathrm{the}} \\ $$$$\boldsymbol{\mathrm{expansion}}\:\boldsymbol{\mathrm{of}}\:\mathrm{100}! \\ $$
Answered by mr W last updated on 01/Oct/20
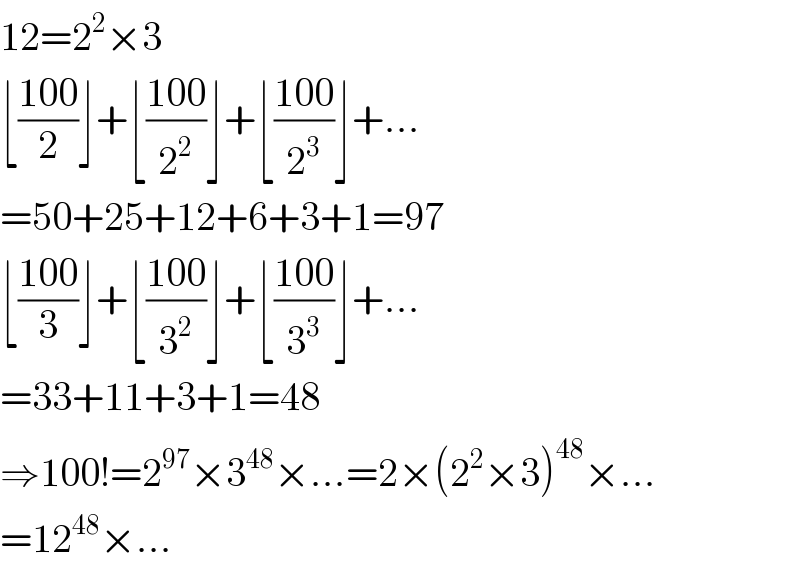
$$\mathrm{12}=\mathrm{2}^{\mathrm{2}} ×\mathrm{3} \\ $$$$\lfloor\frac{\mathrm{100}}{\mathrm{2}}\rfloor+\lfloor\frac{\mathrm{100}}{\mathrm{2}^{\mathrm{2}} }\rfloor+\lfloor\frac{\mathrm{100}}{\mathrm{2}^{\mathrm{3}} }\rfloor+… \\ $$$$=\mathrm{50}+\mathrm{25}+\mathrm{12}+\mathrm{6}+\mathrm{3}+\mathrm{1}=\mathrm{97} \\ $$$$\lfloor\frac{\mathrm{100}}{\mathrm{3}}\rfloor+\lfloor\frac{\mathrm{100}}{\mathrm{3}^{\mathrm{2}} }\rfloor+\lfloor\frac{\mathrm{100}}{\mathrm{3}^{\mathrm{3}} }\rfloor+… \\ $$$$=\mathrm{33}+\mathrm{11}+\mathrm{3}+\mathrm{1}=\mathrm{48} \\ $$$$\Rightarrow\mathrm{100}!=\mathrm{2}^{\mathrm{97}} ×\mathrm{3}^{\mathrm{48}} ×…=\mathrm{2}×\left(\mathrm{2}^{\mathrm{2}} ×\mathrm{3}\right)^{\mathrm{48}} ×… \\ $$$$=\mathrm{12}^{\mathrm{48}} ×… \\ $$
Commented by mr W last updated on 01/Oct/20
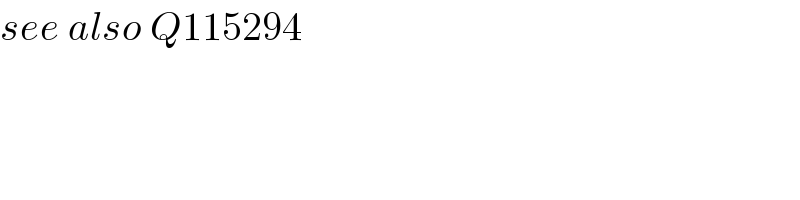
$${see}\:{also}\:{Q}\mathrm{115294} \\ $$
Commented by bemath last updated on 01/Oct/20

$$\mathrm{sir}\:\mathrm{help}\:\mathrm{me}\:\mathrm{qn115988} \\ $$
