Question Number 112664 by bemath last updated on 09/Sep/20

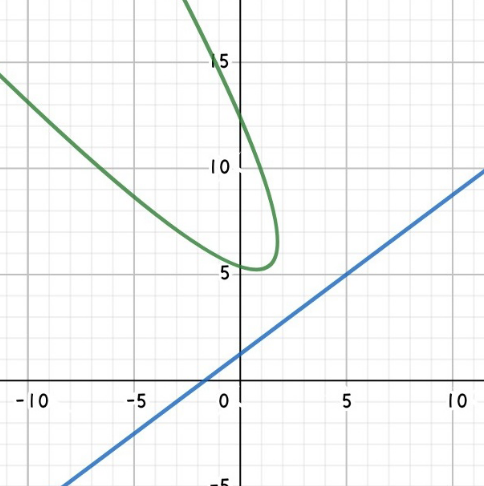
$$\mathrm{what}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{parabola}\: \\ $$$$\mathrm{whose}\:\mathrm{focus}\:\mathrm{F}\left(−\mathrm{3},\mathrm{4}\right)\:\mathrm{and}\:\mathrm{directrix} \\ $$$$\mathrm{is}\:\mathrm{3x}−\mathrm{4y}+\mathrm{5}=\mathrm{0}\:? \\ $$
Commented by bemath last updated on 09/Sep/20
Answered by bobhans last updated on 09/Sep/20
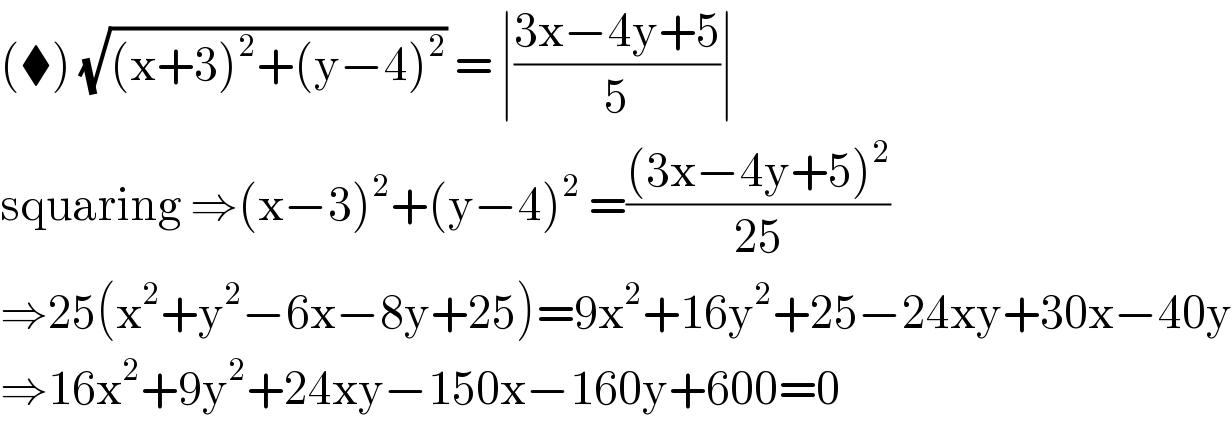
$$\left(\blacklozenge\right)\:\sqrt{\left(\mathrm{x}+\mathrm{3}\right)^{\mathrm{2}} +\left(\mathrm{y}−\mathrm{4}\right)^{\mathrm{2}} }\:=\:\mid\frac{\mathrm{3x}−\mathrm{4y}+\mathrm{5}}{\mathrm{5}}\mid \\ $$$$\mathrm{squaring}\:\Rightarrow\left(\mathrm{x}−\mathrm{3}\right)^{\mathrm{2}} +\left(\mathrm{y}−\mathrm{4}\right)^{\mathrm{2}} \:=\frac{\left(\mathrm{3x}−\mathrm{4y}+\mathrm{5}\right)^{\mathrm{2}} }{\mathrm{25}} \\ $$$$\Rightarrow\mathrm{25}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} −\mathrm{6x}−\mathrm{8y}+\mathrm{25}\right)=\mathrm{9x}^{\mathrm{2}} +\mathrm{16y}^{\mathrm{2}} +\mathrm{25}−\mathrm{24xy}+\mathrm{30x}−\mathrm{40y} \\ $$$$\Rightarrow\mathrm{16x}^{\mathrm{2}} +\mathrm{9y}^{\mathrm{2}} +\mathrm{24xy}−\mathrm{150x}−\mathrm{160y}+\mathrm{600}=\mathrm{0} \\ $$
