Menu Close

what-the-value-of-angle-formed-by-a-long-needle-and-short-needle-on-analog-clock-that-shows-at-15-50-A-175-o-B-174-o-C-173-o-D-172-o-E-170-o-

Tinku Tara 0 Comments
Pin




Question Number 100908 by bemath last updated on 29/Jun/20
what the value of angle formed by a long needle and short needle on analog clock that shows at 15.50 ? (A) 175^o (B) 174^o (C) 173^o (D) 172^o (E) 170^o
$$\mathrm{what}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{angle} \\ $$$$\mathrm{formed}\:\mathrm{by}\:\mathrm{a}\:\mathrm{long}\:\mathrm{needle}\:\mathrm{and}\: \\ $$$$\mathrm{short}\:\mathrm{needle}\:\mathrm{on}\:\mathrm{analog}\:\mathrm{clock}\: \\ $$$$\mathrm{that}\:\mathrm{shows}\:\mathrm{at}\:\mathrm{15}.\mathrm{50}\:? \\ $$$$\left(\mathrm{A}\right)\:\mathrm{175}^{\mathrm{o}} \:\:\:\left(\mathrm{B}\right)\:\mathrm{174}^{\mathrm{o}} \:\:\:\left(\mathrm{C}\right)\:\mathrm{173}^{\mathrm{o}} \\ $$$$\left(\mathrm{D}\right)\:\mathrm{172}^{\mathrm{o}} \:\:\:\:\left(\mathrm{E}\right)\:\mathrm{170}^{\mathrm{o}} \\ $$
Commented by behi83417@gmail.com last updated on 29/Jun/20
θ=∣((11)/2).m−30.h∣ [m=minute,h=houre] 𝛉=∣((11)/2)×50−30×15∣=∣−175∣=175^• ■
$$\theta=\mid\frac{\mathrm{11}}{\mathrm{2}}.\mathrm{m}−\mathrm{30}.\mathrm{h}\mid\:\:\:\:\:\:\:\left[\mathrm{m}=\mathrm{minute},\mathrm{h}=\mathrm{houre}\right] \\ $$$$\boldsymbol{\theta}=\mid\frac{\mathrm{11}}{\mathrm{2}}×\mathrm{50}−\mathrm{30}×\mathrm{15}\mid=\mid−\mathrm{175}\mid=\mathrm{175}^{\bullet} \blacksquare \\ $$
Commented by bemath last updated on 29/Jun/20
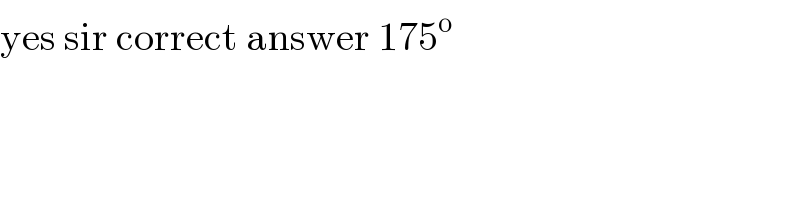
yes sir correct answer 175^o
$$\mathrm{yes}\:\mathrm{sir}\:\mathrm{correct}\:\mathrm{answer}\:\mathrm{175}^{\mathrm{o}} \\ $$
Answered by 1549442205 last updated on 29/Jun/20
At 15 o′clock the long needle′end and short needle′s end are spaced a quarter distance of circle away from each other. The speed of the long needle′s end equal (1/(60))(circle per a minute) and of short needle equal (1/(12×60))(circle per a minute) Hence after 50 minutes the long needle′s end went a distance equal (1/(60))×50=(5/6)(circle) while the short needle′s end went a distance equal 50×(1/(720))=(5/(72))(circle).Therefore, at 15.50 the arc create by ends of both the needles has the length equal (5/6)−((1/4)+(5/(72)))=((37)/(72))(circle)which means that it create an angle has the value equal ((37)/(72))×360°=185° Please,sir check to help me is it correct?
$$\mathrm{At}\:\mathrm{15}\:\mathrm{o}'\mathrm{clock}\:\mathrm{the}\:\mathrm{long}\:\mathrm{needle}'\mathrm{end}\:\:\mathrm{and}\:\mathrm{short} \\ $$$$\mathrm{needle}'\mathrm{s}\:\mathrm{end}\:\mathrm{are}\:\mathrm{spaced}\:\:\mathrm{a}\:\mathrm{quarter}\:\mathrm{distance} \\ $$$$\mathrm{of}\:\mathrm{circle}\:\mathrm{away}\:\mathrm{from}\:\mathrm{each}\:\mathrm{other}. \\ $$$$\mathrm{The}\:\mathrm{speed}\:\mathrm{of}\:\mathrm{the}\:\mathrm{long}\:\mathrm{needle}'\mathrm{s}\:\mathrm{end} \\ $$$$\mathrm{equal}\:\frac{\mathrm{1}}{\mathrm{60}}\left(\mathrm{circle}\:\mathrm{per}\:\mathrm{a}\:\mathrm{minute}\right)\:\mathrm{and}\:\mathrm{of}\: \\ $$$$\mathrm{short}\:\mathrm{needle}\:\mathrm{equal}\:\frac{\mathrm{1}}{\mathrm{12}×\mathrm{60}}\left(\mathrm{circle}\:\mathrm{per}\:\mathrm{a}\:\mathrm{minute}\right) \\ $$$$\mathrm{Hence}\:\mathrm{after}\:\mathrm{50}\:\mathrm{minutes}\:\mathrm{the}\:\mathrm{long}\:\mathrm{needle}'\mathrm{s}\:\mathrm{end} \\ $$$$\mathrm{went}\:\mathrm{a}\:\mathrm{distance}\:\mathrm{equal}\:\frac{\mathrm{1}}{\mathrm{60}}×\mathrm{50}=\frac{\mathrm{5}}{\mathrm{6}}\left(\mathrm{circle}\right) \\ $$$$\mathrm{while}\:\mathrm{the}\:\mathrm{short}\:\mathrm{needle}'\mathrm{s}\:\mathrm{end}\:\mathrm{went}\:\mathrm{a}\:\mathrm{distance} \\ $$$$\mathrm{equal}\:\mathrm{50}×\frac{\mathrm{1}}{\mathrm{720}}=\frac{\mathrm{5}}{\mathrm{72}}\left(\mathrm{circle}\right).\mathrm{Therefore}, \\ $$$$\mathrm{at}\:\mathrm{15}.\mathrm{50}\:\mathrm{the}\:\mathrm{arc}\:\mathrm{create}\:\mathrm{by}\:\mathrm{ends}\:\mathrm{of}\:\mathrm{both} \\ $$$$\mathrm{the}\:\mathrm{needles}\:\mathrm{has}\:\mathrm{the}\:\mathrm{length}\:\mathrm{equal}\: \\ $$$$\frac{\mathrm{5}}{\mathrm{6}}−\left(\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{5}}{\mathrm{72}}\right)=\frac{\mathrm{37}}{\mathrm{72}}\left(\mathrm{circle}\right)\mathrm{which}\:\mathrm{means} \\ $$$$\mathrm{that}\:\mathrm{it}\:\mathrm{create}\:\mathrm{an}\:\mathrm{angle}\:\mathrm{has}\:\mathrm{the}\:\mathrm{value} \\ $$$$\boldsymbol{\mathrm{equal}}\:\frac{\mathrm{37}}{\mathrm{72}}×\mathrm{360}°=\mathrm{185}° \\ $$$$\boldsymbol{\mathrm{Please}},\boldsymbol{\mathrm{sir}}\:\boldsymbol{\mathrm{check}}\:\boldsymbol{\mathrm{to}}\:\boldsymbol{\mathrm{help}}\:\boldsymbol{\mathrm{me}}\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{it}}\:\boldsymbol{\mathrm{correct}}? \\ $$
Commented by bemath last updated on 29/Jun/20
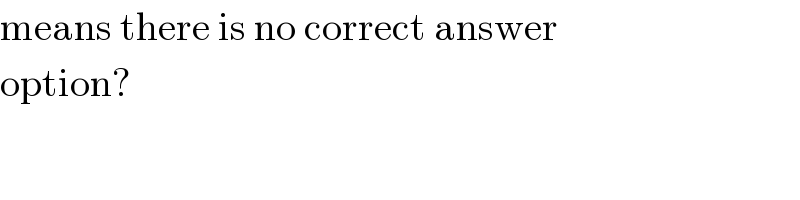
means there is no correct answer option?
$$\mathrm{means}\:\mathrm{there}\:\mathrm{is}\:\mathrm{no}\:\mathrm{correct}\:\mathrm{answer} \\ $$$$\mathrm{option}? \\ $$
Commented by EuclidKaBaap last updated on 29/Jun/20
hahahaha.. its simple thing we often oversee .. its a reflex angle and they havent specified which side.. so 360−185=175 will be the required answer asked in the question
$${hahahaha}..\:\:\:{its}\:{simple}\:{thing}\:{we} \\ $$$${often}\:{oversee}\:..\:{its}\:{a}\:{reflex}\:{angle}\:{and} \\ $$$${they}\:{havent}\:{specified}\:{which}\:{side}.. \\ $$$${so}\:\mathrm{360}−\mathrm{185}=\mathrm{175}\:{will}\:{be}\:{the}\:{required} \\ $$$${answer}\:{asked}\:{in}\:{the}\:{question} \\ $$
Commented by 1549442205 last updated on 29/Jun/20
Thank you sir,a simple thing that I don′t think out !The angle is created by long hand and the short hand (clockwise) equal 360°−185°=175°,so choose answer A:175°
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir},\mathrm{a}\:\mathrm{simple}\:\mathrm{thing}\:\mathrm{that}\:\mathrm{I} \\ $$$$\mathrm{don}'\mathrm{t}\:\mathrm{think}\:\mathrm{out}\:!\mathrm{The}\:\mathrm{angle}\:\mathrm{is}\:\mathrm{created}\:\mathrm{by} \\ $$$$\mathrm{long}\:\mathrm{hand}\:\mathrm{and}\:\mathrm{the}\:\mathrm{short}\:\mathrm{hand}\:\left(\mathrm{clockwise}\right) \\ $$$$\mathrm{equal}\:\mathrm{360}°−\mathrm{185}°=\mathrm{175}°,\mathrm{so}\:\mathrm{choose}\:\mathrm{answer} \\ $$$$\boldsymbol{\mathrm{A}}:\mathrm{175}° \\ $$
Answered by ajfour last updated on 29/Jun/20
At 15:00 angle is 90°. 360° of minute hand ≡ 30° hour hand 300° of minute hand≡ (((300)/(12)))^° hour hand shorter angle between them at 15:50 is = 60°+90°+(((300)/(12)))^° = 175° .
$${At}\:\:\:\mathrm{15}:\mathrm{00}\:\:\:{angle}\:{is}\:\mathrm{90}°. \\ $$$$\mathrm{360}°\:{of}\:{minute}\:{hand}\:\equiv\:\mathrm{30}°\:{hour}\:{hand} \\ $$$$\mathrm{300}°\:{of}\:{minute}\:{hand}\equiv\:\left(\frac{\mathrm{300}}{\mathrm{12}}\right)^{°} {hour}\:{hand} \\ $$$${shorter}\:{angle}\:{between}\:{them}\:{at} \\ $$$$\mathrm{15}:\mathrm{50}\:\:\:{is} \\ $$$$\:\:\:\:\:=\:\mathrm{60}°+\mathrm{90}°+\left(\frac{\mathrm{300}}{\mathrm{12}}\right)^{°} \\ $$$$\:\:\:\:\:=\:\mathrm{175}°\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *