Question Number 55192 by Learner last updated on 19/Feb/19
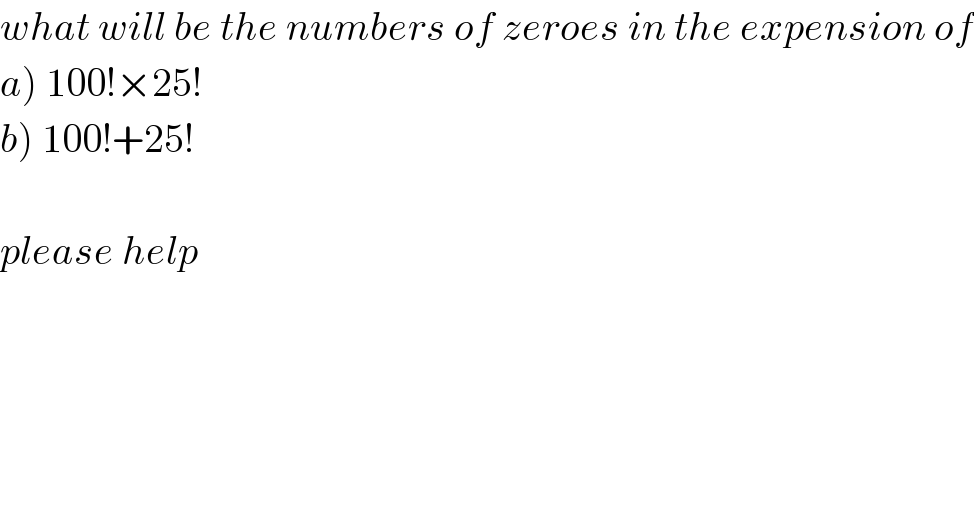
$${what}\:{will}\:{be}\:{the}\:{numbers}\:{of}\:{zeroes}\:{in}\:{the}\:{expension}\:{of} \\ $$$$\left.{a}\right)\:\mathrm{100}!×\mathrm{25}! \\ $$$$\left.{b}\right)\:\mathrm{100}!+\mathrm{25}! \\ $$$$ \\ $$$${please}\:{help} \\ $$
Commented by MJS last updated on 19/Feb/19

$$\mathrm{computed}\:\mathrm{and}\:\mathrm{counted} \\ $$$$\left.\mathrm{a}\right)\:\mathrm{45} \\ $$$$\left.\mathrm{b}\right)\:\mathrm{15} \\ $$$$\mathrm{there}'\mathrm{s}\:\mathrm{no}\:\mathrm{other}\:\mathrm{way}\:\mathrm{to}\:\mathrm{know}\:{all}\:\mathrm{zeros} \\ $$
Answered by kaivan.ahmadi last updated on 19/Feb/19
![n! has [(n/5)]+[(n/5^2 )]+[(n/5^3 )]+... zero in right hand so 100! has [((100)/5)]+[((100)/(25))]+[((100)/(125))]=20+4=24 and 25! has [((25)/5)]+[((25)/(25))]=6 100!×25! has 24×6=144 zero in right hand 100!+25! bas 6 (min{24,6})zero in right hand](https://www.tinkutara.com/question/Q55194.png)
$${n}!\:{has}\:\left[\frac{{n}}{\mathrm{5}}\right]+\left[\frac{{n}}{\mathrm{5}^{\mathrm{2}} }\right]+\left[\frac{{n}}{\mathrm{5}^{\mathrm{3}} }\right]+…\:{zero}\:{in}\:{right}\:{hand} \\ $$$${so}\:\mathrm{100}!\:{has}\:\left[\frac{\mathrm{100}}{\mathrm{5}}\right]+\left[\frac{\mathrm{100}}{\mathrm{25}}\right]+\left[\frac{\mathrm{100}}{\mathrm{125}}\right]=\mathrm{20}+\mathrm{4}=\mathrm{24} \\ $$$${and}\:\:\mathrm{25}!\:{has}\:\left[\frac{\mathrm{25}}{\mathrm{5}}\right]+\left[\frac{\mathrm{25}}{\mathrm{25}}\right]=\mathrm{6}\: \\ $$$$\mathrm{100}!×\mathrm{25}!\:{has}\:\mathrm{24}×\mathrm{6}=\mathrm{144}\:\:{zero}\:{in}\:{right}\:{hand} \\ $$$$\mathrm{100}!+\mathrm{25}!\:{bas}\:\mathrm{6}\:\left({min}\left\{\mathrm{24},\mathrm{6}\right\}\right){zero}\:{in}\:{right}\:{hand} \\ $$
