Question Number 17206 by Arnab Maiti last updated on 02/Jul/17
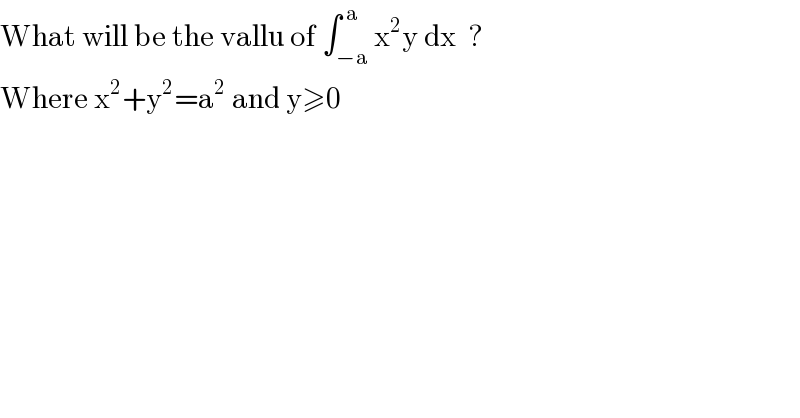
$$\mathrm{What}\:\mathrm{will}\:\mathrm{be}\:\mathrm{the}\:\mathrm{vallu}\:\mathrm{of}\:\int_{−\mathrm{a}} ^{\:\mathrm{a}} \mathrm{x}^{\mathrm{2}} \mathrm{y}\:\mathrm{dx}\:\:? \\ $$$$\mathrm{Where}\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} =\mathrm{a}^{\mathrm{2}} \:\mathrm{and}\:\mathrm{y}\geqslant\mathrm{0} \\ $$
Answered by mrW1 last updated on 02/Jul/17
![let x=a cos θ and y=a sin θ dx=−asin θ dθ x∈[−a,a] and y≥0 ≡θ∈[π,0] ∫_(−a) ^a x^2 ydx=∫_π ^0 a^2 cos^2 θ a sin θ (−asin θ)dθ =−a^4 ∫_π ^0 cos^2 θ sin^2 θ dθ =a^4 ∫_0 ^π cos^2 θ sin^2 θ dθ =(a^4 /4) ∫_0 ^π (2cos θ sin θ)^2 dθ =(a^4 /4) ∫_0 ^π sin^2 2θ dθ =(a^4 /8) ∫_0 ^π [1−cos 4θ ] dθ =(a^4 /8) [θ−(1/4)sin 4θ ]_0 ^π =(a^4 /8)×π =((πa^4 )/8)](https://www.tinkutara.com/question/Q17214.png)
$$\mathrm{let}\:\mathrm{x}=\mathrm{a}\:\mathrm{cos}\:\theta \\ $$$$\mathrm{and}\:\mathrm{y}=\mathrm{a}\:\mathrm{sin}\:\theta \\ $$$$ \\ $$$$\mathrm{dx}=−\mathrm{asin}\:\theta\:\mathrm{d}\theta \\ $$$$\mathrm{x}\in\left[−\mathrm{a},\mathrm{a}\right]\:\mathrm{and}\:\mathrm{y}\geqslant\mathrm{0}\:\equiv\theta\in\left[\pi,\mathrm{0}\right] \\ $$$$ \\ $$$$\int_{−\mathrm{a}} ^{\mathrm{a}} \mathrm{x}^{\mathrm{2}} \mathrm{ydx}=\int_{\pi} ^{\mathrm{0}} \mathrm{a}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta\:\mathrm{a}\:\mathrm{sin}\:\theta\:\left(−\mathrm{asin}\:\theta\right)\mathrm{d}\theta \\ $$$$=−\mathrm{a}^{\mathrm{4}} \:\int_{\pi} ^{\mathrm{0}} \mathrm{cos}^{\mathrm{2}} \:\theta\:\mathrm{sin}^{\mathrm{2}} \:\theta\:\mathrm{d}\theta \\ $$$$=\mathrm{a}^{\mathrm{4}} \:\int_{\mathrm{0}} ^{\pi} \mathrm{cos}^{\mathrm{2}} \:\theta\:\mathrm{sin}^{\mathrm{2}} \:\theta\:\mathrm{d}\theta \\ $$$$=\frac{\mathrm{a}^{\mathrm{4}} }{\mathrm{4}}\:\int_{\mathrm{0}} ^{\pi} \left(\mathrm{2cos}\:\theta\:\mathrm{sin}\:\theta\right)^{\mathrm{2}} \:\mathrm{d}\theta \\ $$$$=\frac{\mathrm{a}^{\mathrm{4}} }{\mathrm{4}}\:\int_{\mathrm{0}} ^{\pi} \:\mathrm{sin}^{\mathrm{2}} \:\mathrm{2}\theta\:\mathrm{d}\theta \\ $$$$=\frac{\mathrm{a}^{\mathrm{4}} }{\mathrm{8}}\:\int_{\mathrm{0}} ^{\pi} \:\left[\mathrm{1}−\mathrm{cos}\:\mathrm{4}\theta\:\right]\:\mathrm{d}\theta \\ $$$$=\frac{\mathrm{a}^{\mathrm{4}} }{\mathrm{8}}\:\left[\theta−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}\:\mathrm{4}\theta\:\right]_{\mathrm{0}} ^{\pi} \\ $$$$=\frac{\mathrm{a}^{\mathrm{4}} }{\mathrm{8}}×\pi \\ $$$$=\frac{\pi\mathrm{a}^{\mathrm{4}} }{\mathrm{8}} \\ $$
Commented by Arnab Maiti last updated on 02/Jul/17

$$\mathscr{E}×\mathfrak{c}\mathrm{ille}^{\mathrm{nt}} !! \\ $$
