When-the-gas-is-ideal-and-process-is-isothermal-then-1-P-1-V-1-P-2-V-2-2-U-0-3-W-0-4-H-1-H-2-

Question Number 23940 by Tinkutara last updated on 10/Nov/17

$$\mathrm{When}\:\mathrm{the}\:\mathrm{gas}\:\mathrm{is}\:\mathrm{ideal}\:\mathrm{and}\:\mathrm{process}\:\mathrm{is} \\ $$$$\mathrm{isothermal},\:\mathrm{then} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{P}_{\mathrm{1}} \mathrm{V}_{\mathrm{1}} \:=\:\mathrm{P}_{\mathrm{2}} \mathrm{V}_{\mathrm{2}} \\ $$$$\left(\mathrm{2}\right)\:\Delta\mathrm{U}\:=\:\mathrm{0} \\ $$$$\left(\mathrm{3}\right)\:\Delta\mathrm{W}\:=\:\mathrm{0} \\ $$$$\left(\mathrm{4}\right)\:\Delta\mathrm{H}_{\mathrm{1}} \:=\:\Delta\mathrm{H}_{\mathrm{2}} \\ $$

Commented by ajfour last updated on 10/Nov/17

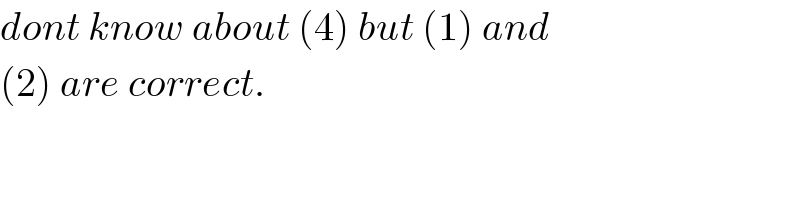
$${dont}\:{know}\:{about}\:\left(\mathrm{4}\right)\:{but}\:\left(\mathrm{1}\right)\:{and} \\ $$$$\left(\mathrm{2}\right)\:{are}\:{correct}. \\ $$

Commented by Tinkutara last updated on 10/Nov/17

$${Now}\:{I}\:{got}\:{the}\:{solution}: \\ $$$$\Delta{H}=\Delta{U}+\Delta\left({PV}\right) \\ $$$${Since}\:\Delta{U}=\mathrm{0}\:{and}\:{PV}\:{is}\:{constant}\:{so} \\ $$$$\Delta{H}_{\mathrm{1}} =\Delta{H}_{\mathrm{2}} =\mathrm{0}. \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com