Question Number 40474 by KMA last updated on 22/Jul/18
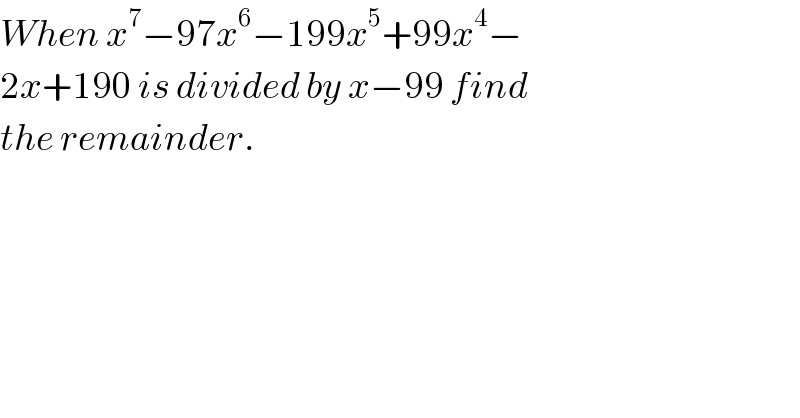
$${When}\:{x}^{\mathrm{7}} −\mathrm{97}{x}^{\mathrm{6}} −\mathrm{199}{x}^{\mathrm{5}} +\mathrm{99}{x}^{\mathrm{4}} − \\ $$$$\mathrm{2}{x}+\mathrm{190}\:{is}\:{divided}\:{by}\:{x}−\mathrm{99}\:{find}\: \\ $$$${the}\:{remainder}. \\ $$
Answered by $@ty@m last updated on 22/Jul/18

Commented by $@ty@m last updated on 22/Jul/18

Answered by math1967 last updated on 22/Jul/18
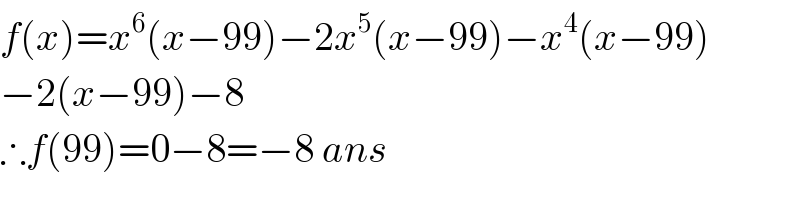
$${f}\left({x}\right)={x}^{\mathrm{6}} \left({x}−\mathrm{99}\right)−\mathrm{2}{x}^{\mathrm{5}} \left({x}−\mathrm{99}\right)−{x}^{\mathrm{4}} \left({x}−\mathrm{99}\right) \\ $$$$−\mathrm{2}\left({x}−\mathrm{99}\right)−\mathrm{8} \\ $$$$\therefore{f}\left(\mathrm{99}\right)=\mathrm{0}−\mathrm{8}=−\mathrm{8}\:{ans} \\ $$
