Menu Close

which-is-correct-5x-4-4x-5-x-5-x-1-2-dx-is-equal-to-a-x-5-x-5-x-1-b-x-1-x-5-x-1-

Tinku Tara 0 Comments
Pin




Question Number 101409 by PRITHWISH SEN 2 last updated on 02/Jul/20
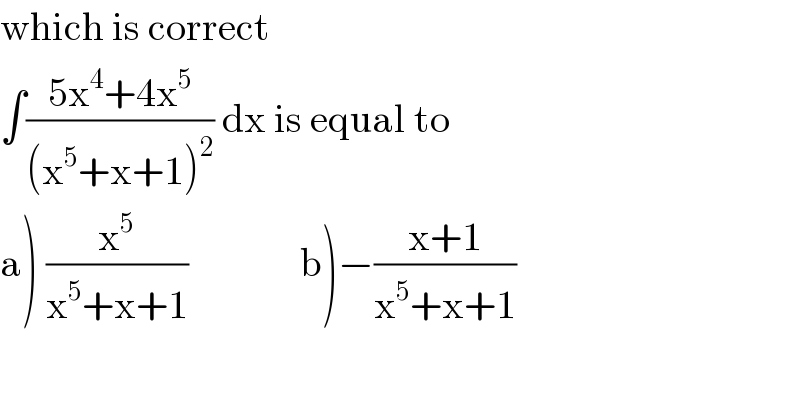
which is correct ∫((5x^4 +4x^5 )/((x^5 +x+1)^2 )) dx is equal to a) (x^5 /(x^5 +x+1)) b)−((x+1)/(x^5 +x+1))
whichiscorrect∫5x4+4x5(x5+x+1)2dxisequaltoa)x5x5+x+1b)−x+1x5+x+1
Commented by Dwaipayan Shikari last updated on 02/Jul/20
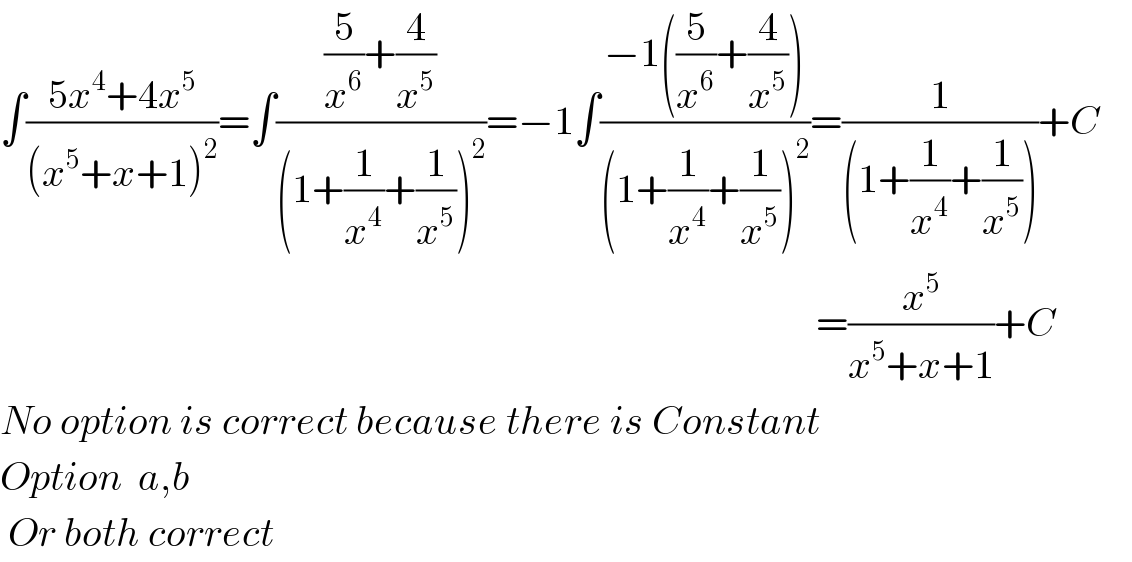
∫((5x^4 +4x^5 )/((x^5 +x+1)^2 ))=∫(((5/x^6 )+(4/x^5 ))/((1+(1/x^4 )+(1/x^5 ))^2 ))=−1∫((−1((5/x^6 )+(4/x^5 )))/((1+(1/x^4 )+(1/x^5 ))^2 ))=(1/((1+(1/x^4 )+(1/x^5 ))))+C =(x^5 /(x^5 +x+1))+C No option is correct because there is Constant Option a,b Or both correct
∫5x4+4x5(x5+x+1)2=∫5x6+4x5(1+1x4+1x5)2=−1∫−1(5x6+4x5)(1+1x4+1x5)2=1(1+1x4+1x5)+C=x5x5+x+1+CNooptioniscorrectbecausethereisConstantOptiona,bOrbothcorrect

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *