Question Number 107905 by aurpeyz last updated on 13/Aug/20

$$\mathrm{W}{hich}\:{of}\:{the}\:{following}\:{set}\:{of}\:{horizontal} \\ $$$${forces}\:{would}\:{lead}\:{an}\:{object}\:{in}\:{equilibrium}? \\ $$$$\left({a}\right)\:\mathrm{5}{N}\:\:\:\mathrm{10}{N}\:\:\mathrm{20}{N} \\ $$$$\left({b}\right)\:\mathrm{6}{N}\:\:\:\mathrm{12}{N}\:\:\:\:\mathrm{18}{N} \\ $$$$\left({c}\right)\:\mathrm{8}{N}\:\:\:\mathrm{8}{N}\:\:\:\mathrm{8}{N} \\ $$$$\left({b}\right)\:\mathrm{2}{N}\:\:\:\:\mathrm{4}{N}\:\:\:\mathrm{8}{N}\:\:\:\mathrm{16}{N} \\ $$
Commented by aurpeyz last updated on 13/Aug/20
$${pls}\:{help}\:{me}\:{with}\:{solution}\:{and}\:{explanation} \\ $$
Commented by mr W last updated on 13/Aug/20

Commented by mr W last updated on 13/Aug/20
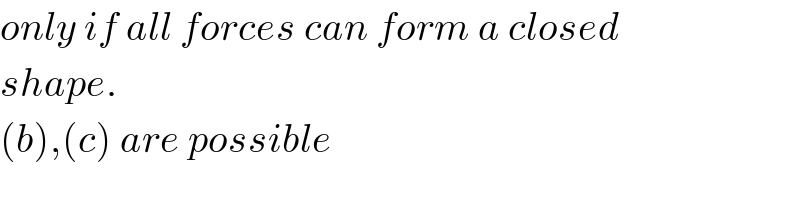
$${only}\:{if}\:{all}\:{forces}\:{can}\:{form}\:{a}\:{closed} \\ $$$${shape}. \\ $$$$\left({b}\right),\left({c}\right)\:{are}\:{possible} \\ $$
Answered by Don08q last updated on 13/Aug/20

$$\mathrm{The}\:\mathrm{object}\:\mathrm{will}\:\mathrm{be}\:\mathrm{in}\:\mathrm{equilibrium}\:\mathrm{if} \\ $$$$\mathrm{and}\:\mathrm{only}\:\mathrm{if}\:\mathrm{one}\:\left({the}\:{resultant}\right)\:\mathrm{of}\:\mathrm{the}\: \\ $$$$\mathrm{forces}\:\mathrm{in}\:\mathrm{any}\:\mathrm{of}\:\mathrm{the}\:\mathrm{sets}\:\mathrm{is}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{the} \\ $$$$\mathrm{algebraic}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{others}.\:\mathrm{In}\:\mathrm{this}\: \\ $$$$\mathrm{case},\:\mathrm{that}\:\mathrm{force}\:\mathrm{must}\:\mathrm{be}\:\mathrm{directed}\:\mathrm{to} \\ $$$$\mathrm{oppose}\:\mathrm{the}\:\mathrm{continuous}\:\mathrm{directions}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{other}\:\mathrm{forces}. \\ $$$$\:\:\left({b}\right)\:\mathrm{6}{N}\:+\:\mathrm{12}{N}\:=\:\mathrm{18}{N} \\ $$$$\:\:\left({d}\right)\:\mathrm{2}{N}\:+\:\mathrm{4}{N}\:+\:\mathrm{8}{N}\:=\:\mathrm{16}{N}\: \\ $$$$ \\ $$
Commented by mr W last updated on 13/Aug/20

$${not}\:{correct}\:{sir}!\:{what}\:{you}\:{said}\:{is}\:{only} \\ $$$${valid}\:{if}\:{all}\:{forces}\:{are}\:{in}\:{the}\:{same} \\ $$$${direction}. \\ $$$${generally}\:{in}\:\mathrm{2}{D}\:{or}\:{in}\:\mathrm{3}{D}, \\ $$$${the}\:{condition}\:{is}\:\Sigma\overset{\rightarrow} {{F}_{{i}} }=\mathrm{0},\:{that}\:{means} \\ $$$${all}\:{forces}\:{should}\:{be}\:{able}\:{to}\:{form}\:{a} \\ $$$${closed}\:{polygon}. \\ $$$$ \\ $$$${besides}\:\mathrm{2}+\mathrm{4}+\mathrm{8}=\mathrm{14}\neq\mathrm{16}! \\ $$
Commented by mr W last updated on 13/Aug/20

Commented by mr W last updated on 13/Aug/20
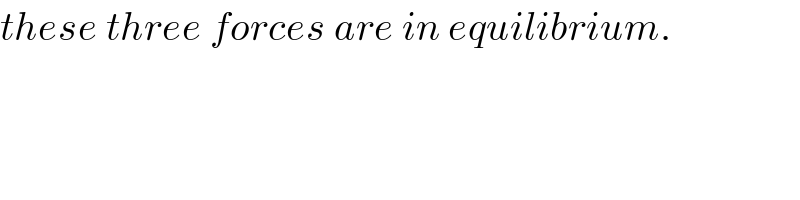
$${these}\:{three}\:{forces}\:{are}\:{in}\:{equilibrium}. \\ $$
Commented by Don08q last updated on 13/Aug/20
$${Yes}.\:{Thanks}\:{for}\:{the}\:{correction} \\ $$
Commented by aurpeyz last updated on 15/Aug/20
$${thanks}\:{for}\:{the}\:{answers} \\ $$
