Question Number 19250 by Tinkutara last updated on 07/Aug/17
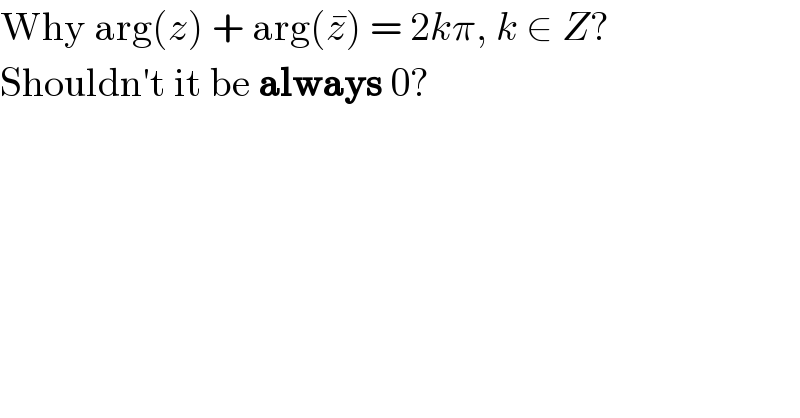
$$\mathrm{Why}\:\mathrm{arg}\left({z}\right)\:+\:\mathrm{arg}\left(\bar {{z}}\right)\:=\:\mathrm{2}{k}\pi,\:{k}\:\in\:{Z}? \\ $$$$\mathrm{Shouldn}'\mathrm{t}\:\mathrm{it}\:\mathrm{be}\:\boldsymbol{\mathrm{always}}\:\mathrm{0}? \\ $$
Commented by ajfour last updated on 07/Aug/17

$$\mathrm{yes},\:\mathrm{so}\:\mathrm{do}\:\mathrm{i}\:\mathrm{think}. \\ $$$$\mathrm{but}\:\mathrm{if}\:{z}=−\mathrm{1}\:?! \\ $$
Commented by Tinkutara last updated on 08/Aug/17
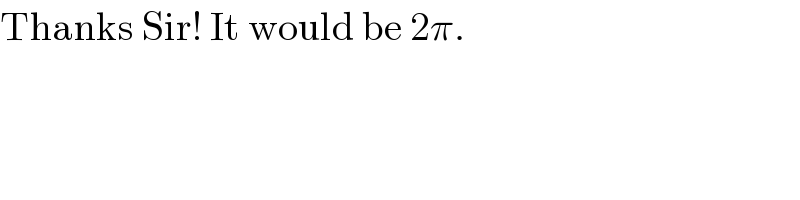
$$\mathrm{Thanks}\:\mathrm{Sir}!\:\mathrm{It}\:\mathrm{would}\:\mathrm{be}\:\mathrm{2}\pi. \\ $$
