Question Number 26772 by Rasheed.Sindhi last updated on 29/Dec/17
$$\mathrm{With}\:\mathrm{a}\:\mathrm{center}\:\boldsymbol{\mathrm{on}}\:\mathrm{a}\:\mathrm{given}\:\mathrm{circle}\:\mathrm{of} \\ $$$$\mathrm{radius}\:\mathrm{r}\:,\mathrm{an}\:\mathrm{arc}\:\mathrm{has}\:\mathrm{been}\:\mathrm{drawn}\:\mathrm{in}\:\mathrm{order} \\ $$$$\mathrm{to}\:\mathrm{divide}\:\mathrm{the}\:\mathrm{circle}\:\mathrm{in}\:\mathrm{two}\:\mathrm{equal} \\ $$$$\left(\mathrm{in}\:\mathrm{area}\right)\:\mathrm{parts}. \\ $$$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{radius}\:\mathrm{of}\:\mathrm{the}\:\mathrm{arc}\:\mathrm{in}\:\mathrm{terms} \\ $$$$\mathrm{of}\:\:\mathrm{r}\:\left(\mathrm{radius}\:\mathrm{of}\:\mathrm{given}\:\mathrm{circle}\right)?\: \\ $$
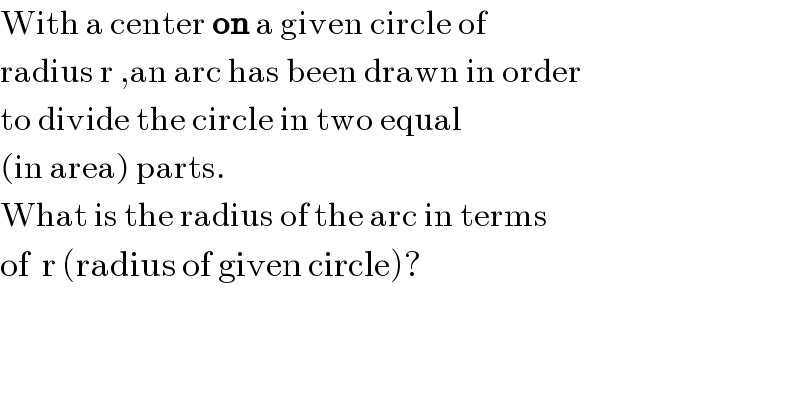
Answered by mrW1 last updated on 29/Dec/17
![Let′s say the radius of the circle is r and the radius of the arc is R. The angle of the arc is θ. r cos (θ/2)=(R/2) ⇒R=2r cos (θ/2) (ϕ/2)=π−2×(θ/2) ⇒ϕ=2π−2θ area of segment of arc BC: A_1 =(R^2 /2)(θ−sin θ)=2r^2 cos^2 (θ/2)(θ−sin θ) area of segment of circle BAC: A_2 =(r^2 /2)[2π−2θ−sin (2π−2θ)]=r^2 (π−θ+sin θ cos θ) A_1 +A_2 =((πr^2 )/2) 2r^2 cos^2 (θ/2)(θ−sin θ)+r^2 (π−θ+sin θ cos θ)=((πr^2 )/2) (cos θ+1)(θ−sin θ)+(π/2)−θ+sin θ cos θ=0 sin θ−θ cos θ=(π/2) ⇒θ≈1.9057 (109.2°) ⇒R=2rcos (θ/2)≈1.16r If the arc divides the area of the circle in ratio λ:1, then the equation is sin θ−θ cos θ=(1−λ)π ⇒λ=1−((sin θ−θ cos θ)/π) cos (θ/2)=(R/(2r))=γ ⇒θ=2 cos^(−1) γ sin (θ/2)=(√(1−γ^2 )) ⇒sin θ=2γ(√(1−γ^2 )) ⇒cos θ=2γ^2 −1 ⇒λ=f(γ)=1−((2γ(√(1−γ^2 ))−2(2γ^2 −1) cos^(−1) γ)/π)](https://www.tinkutara.com/question/Q26773.png)
$${Let}'{s}\:{say}\:{the}\:{radius}\:{of}\:{the}\:{circle}\:{is} \\ $$$${r}\:{and}\:{the}\:{radius}\:{of}\:{the}\:{arc}\:{is}\:{R}. \\ $$$${The}\:{angle}\:{of}\:{the}\:{arc}\:{is}\:\theta. \\ $$$${r}\:\mathrm{cos}\:\frac{\theta}{\mathrm{2}}=\frac{{R}}{\mathrm{2}} \\ $$$$\Rightarrow{R}=\mathrm{2}{r}\:\mathrm{cos}\:\frac{\theta}{\mathrm{2}} \\ $$$$\frac{\varphi}{\mathrm{2}}=\pi−\mathrm{2}×\frac{\theta}{\mathrm{2}} \\ $$$$\Rightarrow\varphi=\mathrm{2}\pi−\mathrm{2}\theta \\ $$$$ \\ $$$${area}\:{of}\:{segment}\:{of}\:{arc}\:{BC}: \\ $$$${A}_{\mathrm{1}} =\frac{{R}^{\mathrm{2}} }{\mathrm{2}}\left(\theta−\mathrm{sin}\:\theta\right)=\mathrm{2}{r}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}\left(\theta−\mathrm{sin}\:\theta\right) \\ $$$${area}\:{of}\:{segment}\:{of}\:{circle}\:{BAC}: \\ $$$${A}_{\mathrm{2}} =\frac{{r}^{\mathrm{2}} }{\mathrm{2}}\left[\mathrm{2}\pi−\mathrm{2}\theta−\mathrm{sin}\:\left(\mathrm{2}\pi−\mathrm{2}\theta\right)\right]={r}^{\mathrm{2}} \left(\pi−\theta+\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta\right) \\ $$$${A}_{\mathrm{1}} +{A}_{\mathrm{2}} =\frac{\pi{r}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\mathrm{2}{r}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}\left(\theta−\mathrm{sin}\:\theta\right)+{r}^{\mathrm{2}} \left(\pi−\theta+\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta\right)=\frac{\pi{r}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\left(\mathrm{cos}\:\theta+\mathrm{1}\right)\left(\theta−\mathrm{sin}\:\theta\right)+\frac{\pi}{\mathrm{2}}−\theta+\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta=\mathrm{0} \\ $$$$\mathrm{sin}\:\theta−\theta\:\mathrm{cos}\:\theta=\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow\theta\approx\mathrm{1}.\mathrm{9057}\:\left(\mathrm{109}.\mathrm{2}°\right) \\ $$$$\Rightarrow{R}=\mathrm{2}{r}\mathrm{cos}\:\frac{\theta}{\mathrm{2}}\approx\mathrm{1}.\mathrm{16}{r} \\ $$$$ \\ $$$${If}\:\:{the}\:{arc}\:{divides}\:{the}\:{area}\:{of}\:{the} \\ $$$${circle}\:{in}\:{ratio}\:\lambda:\mathrm{1},\:{then}\:{the} \\ $$$${equation}\:{is} \\ $$$$\mathrm{sin}\:\theta−\theta\:\mathrm{cos}\:\theta=\left(\mathrm{1}−\lambda\right)\pi \\ $$$$\Rightarrow\lambda=\mathrm{1}−\frac{\mathrm{sin}\:\theta−\theta\:\mathrm{cos}\:\theta}{\pi} \\ $$$$\mathrm{cos}\:\frac{\theta}{\mathrm{2}}=\frac{{R}}{\mathrm{2}{r}}=\gamma \\ $$$$\Rightarrow\theta=\mathrm{2}\:\mathrm{cos}^{−\mathrm{1}} \gamma \\ $$$$\mathrm{sin}\:\frac{\theta}{\mathrm{2}}=\sqrt{\mathrm{1}−\gamma^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{sin}\:\theta=\mathrm{2}\gamma\sqrt{\mathrm{1}−\gamma^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{cos}\:\theta=\mathrm{2}\gamma^{\mathrm{2}} −\mathrm{1} \\ $$$$\Rightarrow\lambda={f}\left(\gamma\right)=\mathrm{1}−\frac{\mathrm{2}\gamma\sqrt{\mathrm{1}−\gamma^{\mathrm{2}} }−\mathrm{2}\left(\mathrm{2}\gamma^{\mathrm{2}} −\mathrm{1}\right)\:\mathrm{cos}^{−\mathrm{1}} \gamma}{\pi} \\ $$
Commented by mrW1 last updated on 29/Dec/17
Commented by Rasheed.Sindhi last updated on 29/Dec/17
$$\mathcal{G}{reat}!\: \\ $$$$\mathcal{T}{han}\mathcal{X}\:\:{a}\:\mathcal{L}{ot}\:\mathcal{S}{ir}! \\ $$
Commented by mrW1 last updated on 29/Dec/17
$${Thank}\:{you}\:{too}\:{Sir}! \\ $$$${But}\:{I}'{m}\:{not}\:{able}\:{to}\:{find}\:{an}\:{analytic} \\ $$$${solution}.\: \\ $$
Commented by mrW1 last updated on 30/Dec/17
$${Sir},\:{do}\:{you}\:{have}\:{any}\:{idea}\:{if}\:{such}\:{an} \\ $$$${arc}\:{can}\:{be}\:{drawn}\:{only}\:{with}\:{ruler}\:{and} \\ $$$${compass}?\:{I}\:{can}\:{hardly}\:{believe}\:{that}\:{it} \\ $$$${is}\:{possible}. \\ $$
Commented by Rasheed.Sindhi last updated on 30/Dec/17
$$\mathrm{To}\:\mathrm{determine}\:\mathrm{area}\:\mathrm{of}\:\mathrm{sector}\:\mathrm{when} \\ $$$$\mathrm{coordinates}\:\mathrm{of}\:\mathrm{three}\:\mathrm{specifying} \\ $$$$\mathrm{points}\:\mathrm{are}\:\mathrm{given}.\:\mathrm{What}'\mathrm{s}\:\mathrm{the}\: \\ $$$$\mathrm{formula}? \\ $$
Commented by Rasheed.Sindhi last updated on 30/Dec/17
$$\mathrm{Sorry}\:\mathrm{it}'\mathrm{s}\:\mathrm{not}\:\mathrm{only}\:\mathrm{matter}\:\mathrm{of}\: \\ $$$$\mathrm{sector}\:\mathrm{area}! \\ $$
Commented by mrW1 last updated on 30/Dec/17
$${I}\:{don}'{t}\:{know}\:{such}\:{a}\:{formula}. \\ $$
Commented by Rasheed.Sindhi last updated on 30/Dec/17
$$\mathrm{No}\:\mathrm{sir},\:\mathrm{I}\:\mathrm{myself}\:\mathrm{am}\:\mathrm{not}\:\mathrm{sure}! \\ $$$$\mathrm{Mr}\:\mathrm{prakash}\:\mathrm{jain}\:\mathrm{can}\:\mathrm{certainly} \\ $$$$\mathrm{say}\:\mathrm{something}. \\ $$
Commented by prakash jain last updated on 30/Dec/17
$$\mathrm{I}\:\mathrm{am}\:\mathrm{still}\:\mathrm{thinking}\:\mathrm{about}\:\mathrm{that} \\ $$$$\mathrm{problem}. \\ $$