without-beta-function-cos-3-t-sin-2-t-dt-

Question Number 64320 by aliesam last updated on 16/Jul/19

w i t h o u t b e t a f u n c t i o n

\int {c o s}^{3} t {s i n}^{2} t d t

Commented by mathmax by abdo last updated on 16/Jul/19

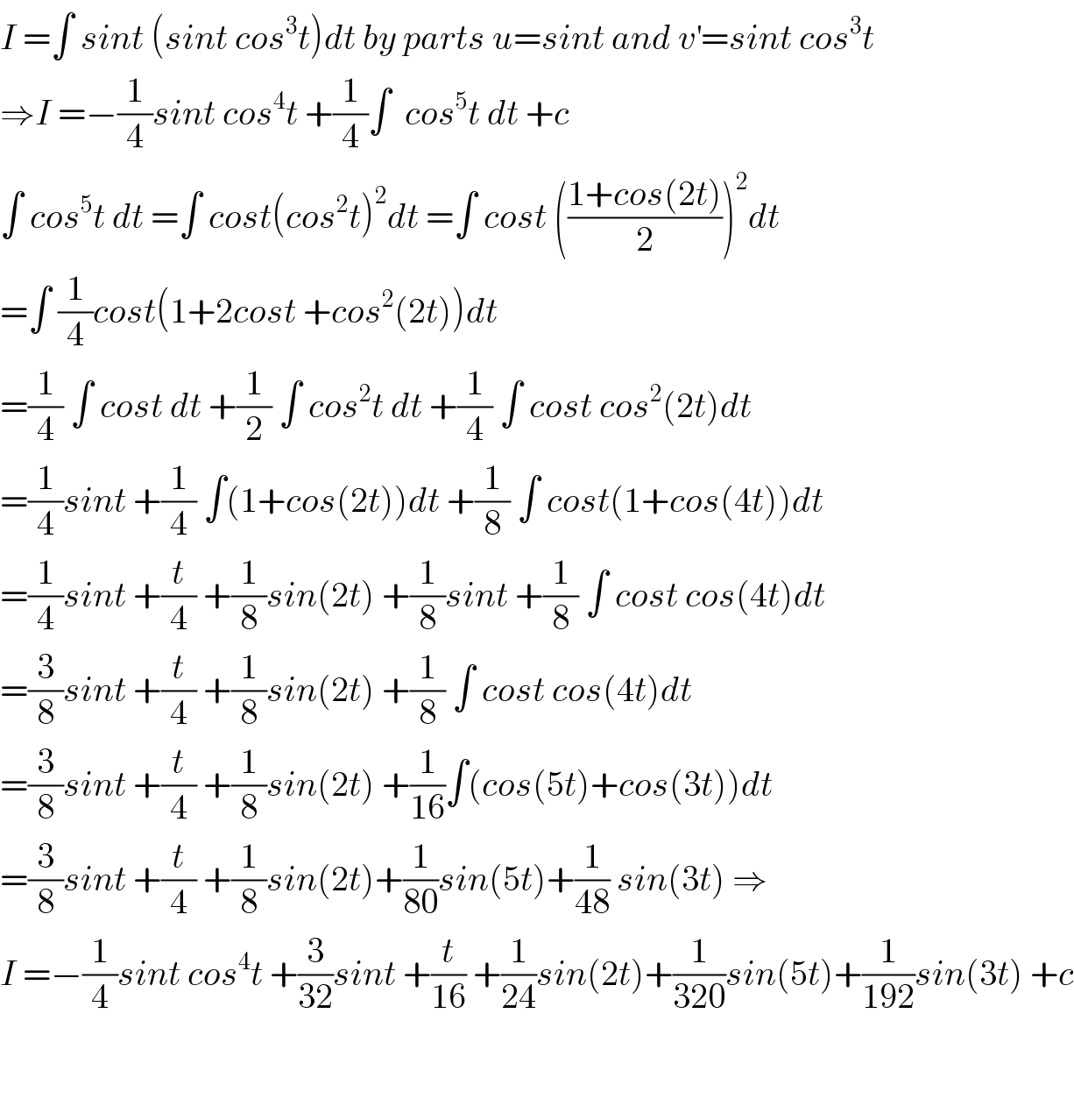
I = \int s i n t (s i n t {c o s}^{3} t) d t b y p a r t s u = s i n t a n d v^{^{'}} = s i n t {c o s}^{3} t

\Rightarrow I = - \frac{1}{4} s i n t {c o s}^{4} t + \frac{1}{4} \int {c o s}^{5} t d t + c

\int {c o s}^{5} t d t = \int c o s t {({c o s}^{2} t)}^{2} d t = \int c o s t {(\frac{1 + c o s (2 t)}{2})}^{2} d t

= \int \frac{1}{4} c o s t (1 + 2 c o s t + {c o s}^{2} (2 t)) d t

= \frac{1}{4} \int c o s t d t + \frac{1}{2} \int {c o s}^{2} t d t + \frac{1}{4} \int c o s t {c o s}^{2} (2 t) d t

= \frac{1}{4} s i n t + \frac{1}{4} \int (1 + c o s (2 t)) d t + \frac{1}{8} \int c o s t (1 + c o s (4 t)) d t

= \frac{1}{4} s i n t + \frac{t}{4} + \frac{1}{8} s i n (2 t) + \frac{1}{8} s i n t + \frac{1}{8} \int c o s t c o s (4 t) d t

= \frac{3}{8} s i n t + \frac{t}{4} + \frac{1}{8} s i n (2 t) + \frac{1}{8} \int c o s t c o s (4 t) d t

= \frac{3}{8} s i n t + \frac{t}{4} + \frac{1}{8} s i n (2 t) + \frac{1}{16} \int (c o s (5 t) + c o s (3 t)) d t

= \frac{3}{8} s i n t + \frac{t}{4} + \frac{1}{8} s i n (2 t) + \frac{1}{80} s i n (5 t) + \frac{1}{48} s i n (3 t) \Rightarrow

I = - \frac{1}{4} s i n t {c o s}^{4} t + \frac{3}{32} s i n t + \frac{t}{16} + \frac{1}{24} s i n (2 t) + \frac{1}{320} s i n (5 t) + \frac{1}{192} s i n (3 t) + c

Answered by Tanmay chaudhury last updated on 16/Jul/19

\int (1 - {s i n}^{2} t) {s i n}^{2} t c o s t d t

\int (a^{2} - a^{4}) d a a = s i n t d a = c o s t d t

\frac{a^{3}}{3} - \frac{a^{5}}{5} + c

\frac{{s i n}^{3} t}{3} - \frac{{s i n}^{5} t}{5} + c