Menu Close

Without-L-Hopital-lim-x-pi-7-sin-x-sin-2x-sin-3x-7-8-x-pi-7-

Tinku Tara 0 Comments
Pin




Question Number 149596 by iloveisrael last updated on 06/Aug/21
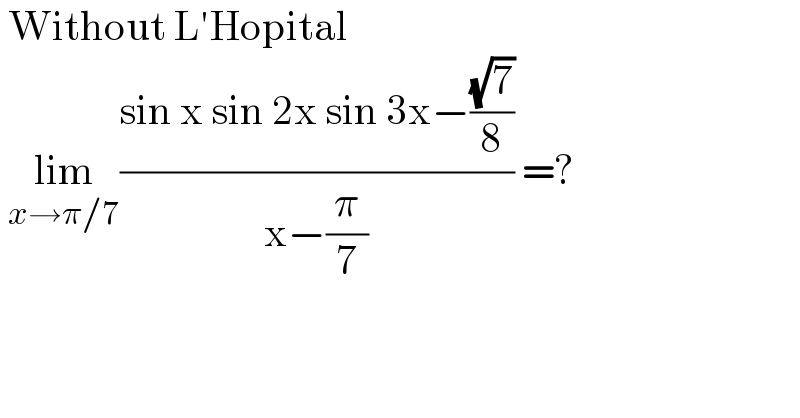
Without L′Hopital lim_(x→π/7) ((sin x sin 2x sin 3x−((√7)/8))/(x−(π/7))) =?
$$\:\mathrm{Without}\:\mathrm{L}'\mathrm{Hopital} \\ $$$$\:\underset{{x}\rightarrow\pi/\mathrm{7}} {\mathrm{lim}}\frac{\mathrm{sin}\:\mathrm{x}\:\mathrm{sin}\:\mathrm{2x}\:\mathrm{sin}\:\mathrm{3x}−\frac{\sqrt{\mathrm{7}}}{\mathrm{8}}}{\mathrm{x}−\frac{\pi}{\mathrm{7}}}\:=? \\ $$
Answered by EDWIN88 last updated on 07/Aug/21
let x−(π/7)=t ; x=t+(π/7) ∧ t→0 lim_(t→0) ((sin (t+(π/7))sin (2t+((2π)/7))sin (3t+((3π)/7))−((√7)/8))/t) =lim_(t→0) ((8sin (t+(π/7))sin (2t+((2π)/7))sin (3t+((3π)/7))−(√7))/(8t)) =lim_(t→0) ((−4sin (2t+((2π)/7)){cos (2t+((2π)/7))−cos (t+(π/7))}−(√7))/(8t)) =lim_(t→0) ((−2sin (4t+((4π)/7))+4sin (2t+((2π)/7))cos (t+(π/7))−(√7))/(8t)) =lim_(t→0) ((−2sin (4t+((4π)/7))+2(sin (3t+((3π)/7))+sin (t+(π/7)))−(√7))/(8t)) =lim_(t→0) ((−2sin (4t+((4π)/7))+2sin (3t+((3π)/7))+2sin (t+(π/7))−(√7))/(8t)) =lim_(t→0) ((−8cos (4t+((4π)/7))+6cos (3t+((3π)/7))+2cos (t+(π/7)))/8) =−8cos ((4π)/7)+6cos ((3π)/7)+2cos (π/7) (•)cos ((4π)/7)=cos (π−((3π)/( 7)))=−cos ((3π)/7) =8cos ((3π)/7)+6cos ((3π)/7)+2cos (π/7) =14cos ((3π)/7)+2cos (π/7) L=((14cos ((3π)/7)+2cos (π/7))/8) ≈ 0.614654
$$\: \\ $$$$\mathrm{let}\:{x}−\frac{\pi}{\mathrm{7}}={t}\:;\:{x}={t}+\frac{\pi}{\mathrm{7}}\:\wedge\:{t}\rightarrow\mathrm{0} \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:\left({t}+\frac{\pi}{\mathrm{7}}\right)\mathrm{sin}\:\left(\mathrm{2}{t}+\frac{\mathrm{2}\pi}{\mathrm{7}}\right)\mathrm{sin}\:\left(\mathrm{3}{t}+\frac{\mathrm{3}\pi}{\mathrm{7}}\right)−\frac{\sqrt{\mathrm{7}}}{\mathrm{8}}}{{t}} \\ $$$$=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{8sin}\:\left({t}+\frac{\pi}{\mathrm{7}}\right)\mathrm{sin}\:\left(\mathrm{2}{t}+\frac{\mathrm{2}\pi}{\mathrm{7}}\right)\mathrm{sin}\:\left(\mathrm{3}{t}+\frac{\mathrm{3}\pi}{\mathrm{7}}\right)−\sqrt{\mathrm{7}}}{\mathrm{8}{t}} \\ $$$$=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{4sin}\:\left(\mathrm{2}{t}+\frac{\mathrm{2}\pi}{\mathrm{7}}\right)\left\{\mathrm{cos}\:\left(\mathrm{2}{t}+\frac{\mathrm{2}\pi}{\mathrm{7}}\right)−\mathrm{cos}\:\left({t}+\frac{\pi}{\mathrm{7}}\right)\right\}−\sqrt{\mathrm{7}}}{\mathrm{8}{t}} \\ $$$$=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{2sin}\:\left(\mathrm{4}{t}+\frac{\mathrm{4}\pi}{\mathrm{7}}\right)+\mathrm{4sin}\:\left(\mathrm{2}{t}+\frac{\mathrm{2}\pi}{\mathrm{7}}\right)\mathrm{cos}\:\left({t}+\frac{\pi}{\mathrm{7}}\right)−\sqrt{\mathrm{7}}}{\mathrm{8}{t}} \\ $$$$=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{2sin}\:\left(\mathrm{4}{t}+\frac{\mathrm{4}\pi}{\mathrm{7}}\right)+\mathrm{2}\left(\mathrm{sin}\:\left(\mathrm{3}{t}+\frac{\mathrm{3}\pi}{\mathrm{7}}\right)+\mathrm{sin}\:\left({t}+\frac{\pi}{\mathrm{7}}\right)\right)−\sqrt{\mathrm{7}}}{\mathrm{8}{t}} \\ $$$$=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{2sin}\:\left(\mathrm{4}{t}+\frac{\mathrm{4}\pi}{\mathrm{7}}\right)+\mathrm{2sin}\:\left(\mathrm{3}{t}+\frac{\mathrm{3}\pi}{\mathrm{7}}\right)+\mathrm{2sin}\:\left({t}+\frac{\pi}{\mathrm{7}}\right)−\sqrt{\mathrm{7}}}{\mathrm{8}{t}} \\ $$$$=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{8cos}\:\left(\mathrm{4}{t}+\frac{\mathrm{4}\pi}{\mathrm{7}}\right)+\mathrm{6cos}\:\left(\mathrm{3}{t}+\frac{\mathrm{3}\pi}{\mathrm{7}}\right)+\mathrm{2cos}\:\left({t}+\frac{\pi}{\mathrm{7}}\right)}{\mathrm{8}} \\ $$$$=−\mathrm{8cos}\:\frac{\mathrm{4}\pi}{\mathrm{7}}+\mathrm{6cos}\:\frac{\mathrm{3}\pi}{\mathrm{7}}+\mathrm{2cos}\:\frac{\pi}{\mathrm{7}} \\ $$$$\left(\bullet\right)\mathrm{cos}\:\frac{\mathrm{4}\pi}{\mathrm{7}}=\mathrm{cos}\:\left(\pi−\frac{\mathrm{3}\pi}{\:\mathrm{7}}\right)=−\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{7}} \\ $$$$=\mathrm{8cos}\:\frac{\mathrm{3}\pi}{\mathrm{7}}+\mathrm{6cos}\:\frac{\mathrm{3}\pi}{\mathrm{7}}+\mathrm{2cos}\:\frac{\pi}{\mathrm{7}} \\ $$$$=\mathrm{14cos}\:\frac{\mathrm{3}\pi}{\mathrm{7}}+\mathrm{2cos}\:\frac{\pi}{\mathrm{7}} \\ $$$${L}=\frac{\mathrm{14cos}\:\frac{\mathrm{3}\pi}{\mathrm{7}}+\mathrm{2cos}\:\frac{\pi}{\mathrm{7}}}{\mathrm{8}}\:\approx\:\mathrm{0}.\mathrm{614654} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *