Question Number 145363 by imjagoll last updated on 04/Jul/21
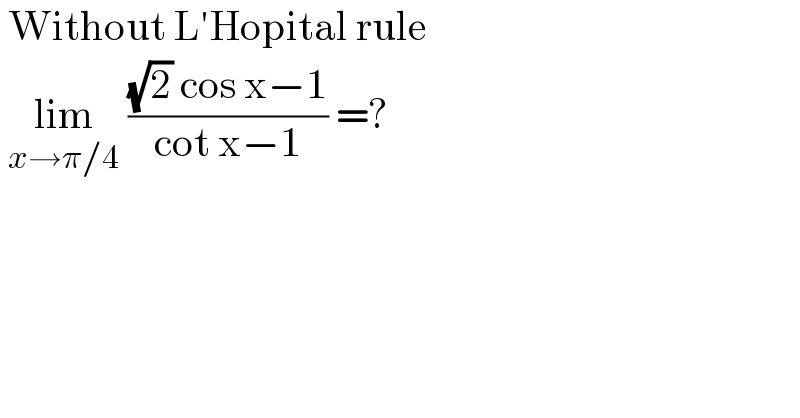
$$\:\mathrm{Without}\:\mathrm{L}'\mathrm{Hopital}\:\mathrm{rule} \\ $$$$\:\underset{{x}\rightarrow\pi/\mathrm{4}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{2}}\:\mathrm{cos}\:\mathrm{x}−\mathrm{1}}{\mathrm{cot}\:\mathrm{x}−\mathrm{1}}\:=? \\ $$
Answered by liberty last updated on 04/Jul/21
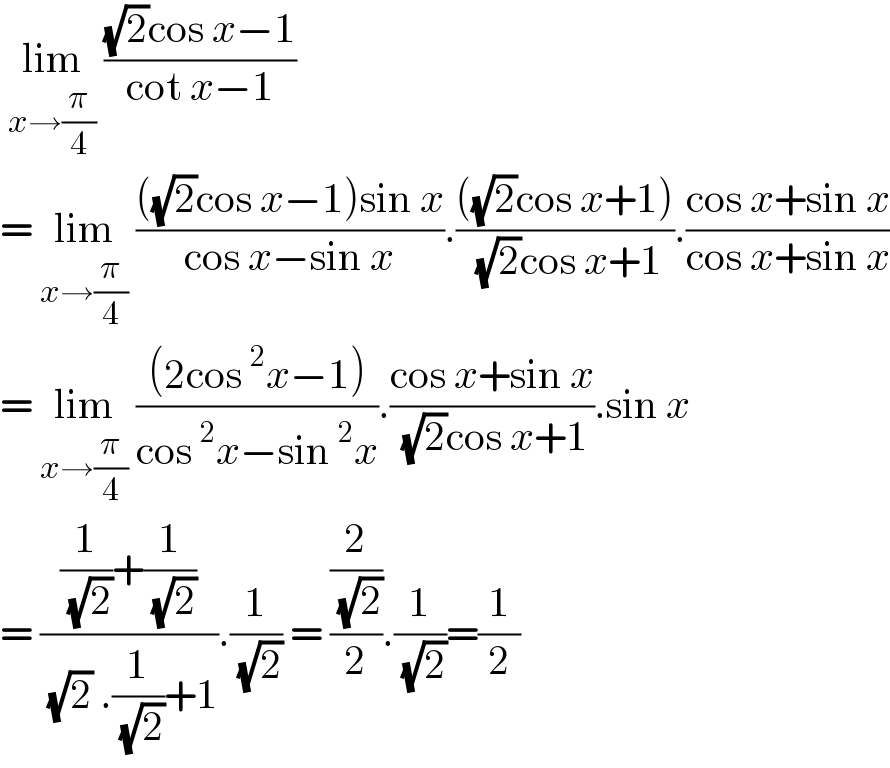
$$\:\underset{{x}\rightarrow\frac{\pi}{\mathrm{4}}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{2}}\mathrm{cos}\:{x}−\mathrm{1}}{\mathrm{cot}\:{x}−\mathrm{1}}\: \\ $$$$=\:\underset{{x}\rightarrow\frac{\pi}{\mathrm{4}}} {\mathrm{lim}}\:\frac{\left(\sqrt{\mathrm{2}}\mathrm{cos}\:{x}−\mathrm{1}\right)\mathrm{sin}\:{x}}{\mathrm{cos}\:{x}−\mathrm{sin}\:{x}}.\frac{\left(\sqrt{\mathrm{2}}\mathrm{cos}\:{x}+\mathrm{1}\right)}{\:\sqrt{\mathrm{2}}\mathrm{cos}\:{x}+\mathrm{1}}.\frac{\mathrm{cos}\:{x}+\mathrm{sin}\:{x}}{\mathrm{cos}\:{x}+\mathrm{sin}\:{x}} \\ $$$$=\:\underset{{x}\rightarrow\frac{\pi}{\mathrm{4}}} {\mathrm{lim}}\:\frac{\left(\mathrm{2cos}\:^{\mathrm{2}} {x}−\mathrm{1}\right)}{\mathrm{cos}\:^{\mathrm{2}} {x}−\mathrm{sin}\:^{\mathrm{2}} {x}}.\frac{\mathrm{cos}\:{x}+\mathrm{sin}\:{x}}{\:\sqrt{\mathrm{2}}\mathrm{cos}\:{x}+\mathrm{1}}.\mathrm{sin}\:{x} \\ $$$$=\:\frac{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}}{\:\sqrt{\mathrm{2}}\:.\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}+\mathrm{1}}.\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:=\:\frac{\frac{\mathrm{2}}{\:\sqrt{\mathrm{2}}}}{\mathrm{2}}.\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Answered by puissant last updated on 04/Jul/21
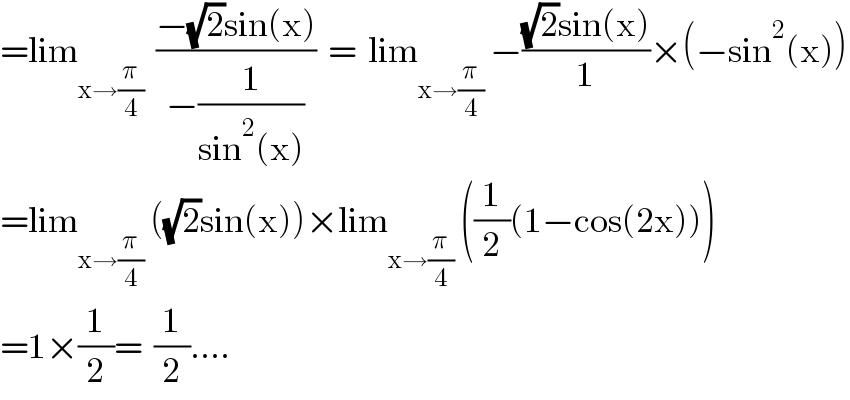
$$=\mathrm{lim}_{\mathrm{x}\rightarrow\frac{\pi}{\mathrm{4}}} \:\:\frac{−\sqrt{\mathrm{2}}\mathrm{sin}\left(\mathrm{x}\right)}{−\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} \left(\mathrm{x}\right)}}\:\:=\:\:\mathrm{lim}_{\mathrm{x}\rightarrow\frac{\pi}{\mathrm{4}}} \:−\frac{\sqrt{\mathrm{2}}\mathrm{sin}\left(\mathrm{x}\right)}{\mathrm{1}}×\left(−\mathrm{sin}^{\mathrm{2}} \left(\mathrm{x}\right)\right) \\ $$$$=\mathrm{lim}_{\mathrm{x}\rightarrow\frac{\pi}{\mathrm{4}}} \:\left(\sqrt{\mathrm{2}}\mathrm{sin}\left(\mathrm{x}\right)\right)×\mathrm{lim}_{\mathrm{x}\rightarrow\frac{\pi}{\mathrm{4}}} \:\left(\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\mathrm{cos}\left(\mathrm{2x}\right)\right)\right) \\ $$$$=\mathrm{1}×\frac{\mathrm{1}}{\mathrm{2}}=\:\:\frac{\mathrm{1}}{\mathrm{2}}…. \\ $$
Answered by Olaf_Thorendsen last updated on 04/Jul/21
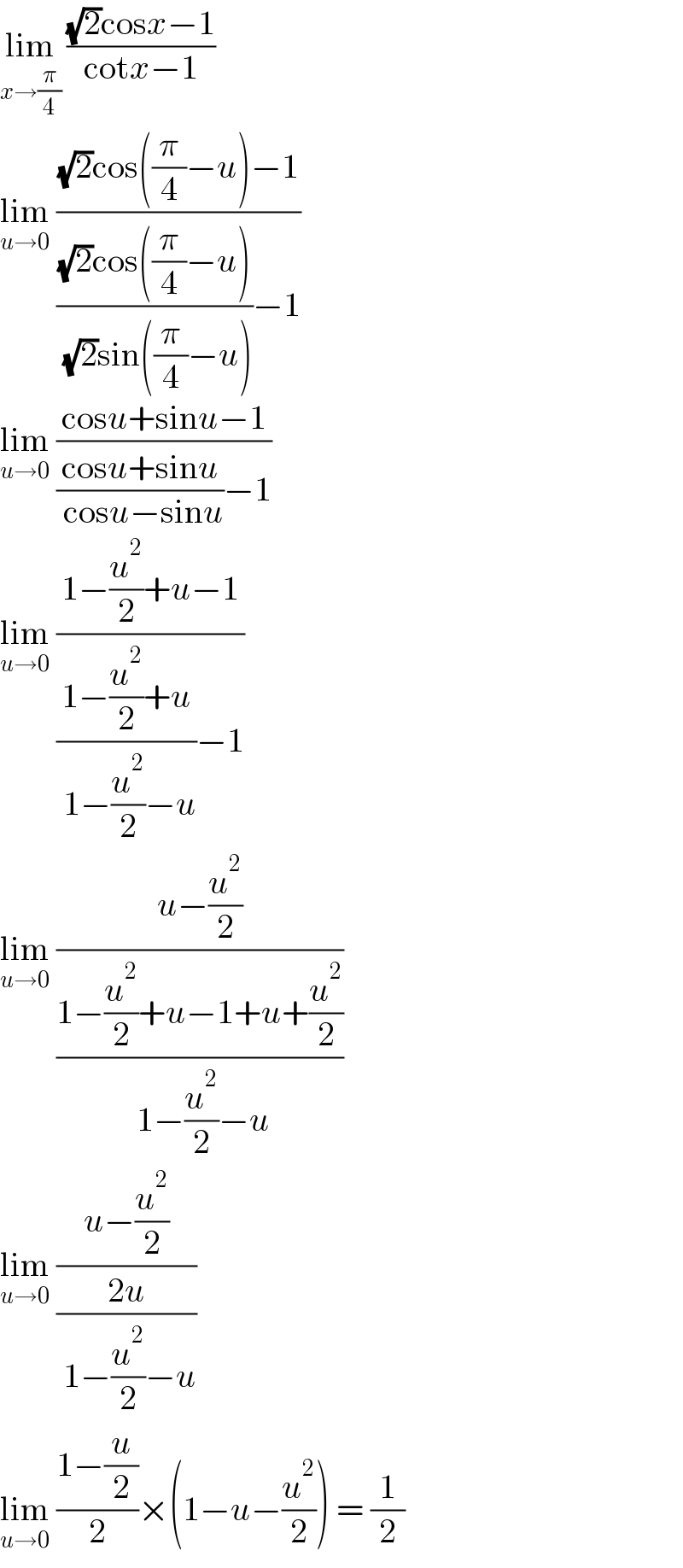
$$\underset{{x}\rightarrow\frac{\pi}{\mathrm{4}}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{2}}\mathrm{cos}{x}−\mathrm{1}}{\mathrm{cot}{x}−\mathrm{1}} \\ $$$$\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{2}}\mathrm{cos}\left(\frac{\pi}{\mathrm{4}}−{u}\right)−\mathrm{1}}{\frac{\sqrt{\mathrm{2}}\mathrm{cos}\left(\frac{\pi}{\mathrm{4}}−{u}\right)}{\:\sqrt{\mathrm{2}}\mathrm{sin}\left(\frac{\pi}{\mathrm{4}}−{u}\right)}−\mathrm{1}} \\ $$$$\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{cos}{u}+\mathrm{sin}{u}−\mathrm{1}}{\frac{\mathrm{cos}{u}+\mathrm{sin}{u}}{\:\mathrm{cos}{u}−\mathrm{sin}{u}}−\mathrm{1}} \\ $$$$\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\frac{{u}^{\mathrm{2}} }{\mathrm{2}}+{u}−\mathrm{1}}{\frac{\mathrm{1}−\frac{{u}^{\mathrm{2}} }{\mathrm{2}}+{u}}{\:\mathrm{1}−\frac{{u}^{\mathrm{2}} }{\mathrm{2}}−{u}}−\mathrm{1}} \\ $$$$\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{u}−\frac{{u}^{\mathrm{2}} }{\mathrm{2}}}{\frac{\mathrm{1}−\frac{{u}^{\mathrm{2}} }{\mathrm{2}}+{u}−\mathrm{1}+{u}+\frac{{u}^{\mathrm{2}} }{\mathrm{2}}}{\:\mathrm{1}−\frac{{u}^{\mathrm{2}} }{\mathrm{2}}−{u}}} \\ $$$$\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{u}−\frac{{u}^{\mathrm{2}} }{\mathrm{2}}}{\frac{\mathrm{2}{u}}{\:\mathrm{1}−\frac{{u}^{\mathrm{2}} }{\mathrm{2}}−{u}}} \\ $$$$\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\frac{{u}}{\mathrm{2}}}{\mathrm{2}}×\left(\mathrm{1}−{u}−\frac{{u}^{\mathrm{2}} }{\mathrm{2}}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$
