Question Number 111583 by Rio Michael last updated on 04/Sep/20
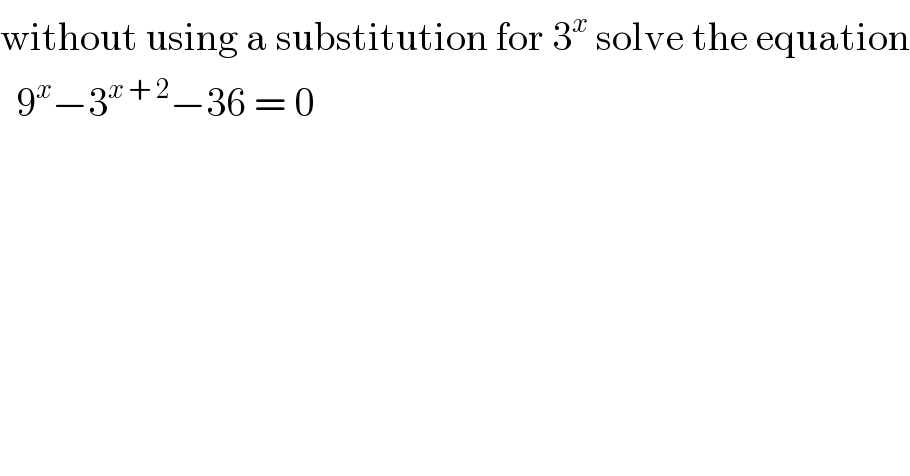
$$\mathrm{without}\:\mathrm{using}\:\mathrm{a}\:\mathrm{substitution}\:\mathrm{for}\:\mathrm{3}^{{x}} \:\mathrm{solve}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\:\:\mathrm{9}^{{x}} −\mathrm{3}^{{x}\:+\:\mathrm{2}} −\mathrm{36}\:=\:\mathrm{0} \\ $$
Answered by bemath last updated on 04/Sep/20
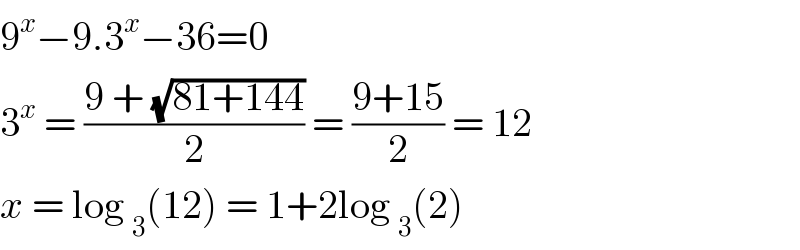
$$\mathrm{9}^{{x}} −\mathrm{9}.\mathrm{3}^{{x}} −\mathrm{36}=\mathrm{0} \\ $$$$\mathrm{3}^{{x}} \:=\:\frac{\mathrm{9}\:+\:\sqrt{\mathrm{81}+\mathrm{144}}}{\mathrm{2}}\:=\:\frac{\mathrm{9}+\mathrm{15}}{\mathrm{2}}\:=\:\mathrm{12} \\ $$$${x}\:=\:\mathrm{log}\:_{\mathrm{3}} \left(\mathrm{12}\right)\:=\:\mathrm{1}+\mathrm{2log}\:_{\mathrm{3}} \left(\mathrm{2}\right) \\ $$
Commented by Rio Michael last updated on 04/Sep/20
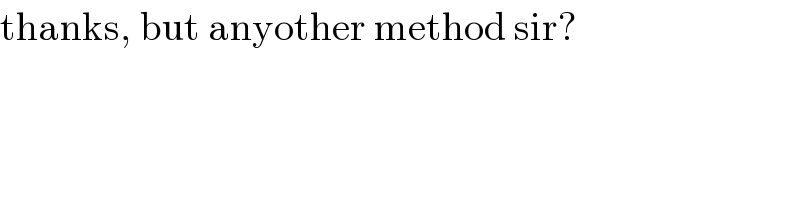
$$\mathrm{thanks},\:\mathrm{but}\:\mathrm{anyother}\:\mathrm{method}\:\mathrm{sir}? \\ $$
