Question Number 51235 by peter frank last updated on 25/Dec/18
$${Without}\:{using}\:{tables}, \\ $$$${find}\:{tha}\:{value}\:{of} \\ $$$$\frac{\left(\sqrt{\mathrm{5}}\:+\mathrm{2}\right)^{\mathrm{6}} −\left(\sqrt{\mathrm{5}}−\mathrm{2}\right)^{\mathrm{6}} }{\mathrm{8}\sqrt{\mathrm{5}}\:}\:\: \\ $$
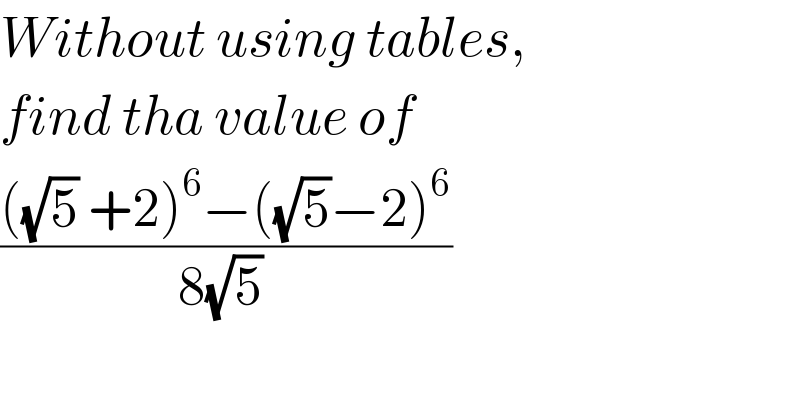
Answered by mr W last updated on 25/Dec/18
![let a=(√5)+2 (√5)−2=(1/( (√5)+2))=(1/a) a^6 −(1/a^6 )=(a^3 +(1/a^3 ))(a^3 −(1/a^3 ))=(a+(1/a))(a^2 +(1/a^2 )−1)(a−(1/a))(a^2 +(1/a^2 )+1) =(a^2 −(1/a^2 ))[(a^2 +(1/a^2 ))^2 −1] =(8(√5))(18^2 −1) ⇒((((√5) +2)^6 −((√5)−2)^6 )/(8(√5) ))=18^2 −1 =17×19=323](https://www.tinkutara.com/question/Q51249.png)
$${let}\:{a}=\sqrt{\mathrm{5}}+\mathrm{2} \\ $$$$\sqrt{\mathrm{5}}−\mathrm{2}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}+\mathrm{2}}=\frac{\mathrm{1}}{{a}} \\ $$$${a}^{\mathrm{6}} −\frac{\mathrm{1}}{{a}^{\mathrm{6}} }=\left({a}^{\mathrm{3}} +\frac{\mathrm{1}}{{a}^{\mathrm{3}} }\right)\left({a}^{\mathrm{3}} −\frac{\mathrm{1}}{{a}^{\mathrm{3}} }\right)=\left({a}+\frac{\mathrm{1}}{{a}}\right)\left({a}^{\mathrm{2}} +\frac{\mathrm{1}}{{a}^{\mathrm{2}} }−\mathrm{1}\right)\left({a}−\frac{\mathrm{1}}{{a}}\right)\left({a}^{\mathrm{2}} +\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\mathrm{1}\right) \\ $$$$=\left({a}^{\mathrm{2}} −\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\right)\left[\left({a}^{\mathrm{2}} +\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\right)^{\mathrm{2}} −\mathrm{1}\right] \\ $$$$=\left(\mathrm{8}\sqrt{\mathrm{5}}\right)\left(\mathrm{18}^{\mathrm{2}} −\mathrm{1}\right) \\ $$$$\Rightarrow\frac{\left(\sqrt{\mathrm{5}}\:+\mathrm{2}\right)^{\mathrm{6}} −\left(\sqrt{\mathrm{5}}−\mathrm{2}\right)^{\mathrm{6}} }{\mathrm{8}\sqrt{\mathrm{5}}\:}=\mathrm{18}^{\mathrm{2}} −\mathrm{1}\:\: \\ $$$$=\mathrm{17}×\mathrm{19}=\mathrm{323} \\ $$
Commented by peter frank last updated on 25/Dec/18
$${much}\:{respect}\:{sir}\:{nice}\:{work} \\ $$
Commented by malwaan last updated on 25/Dec/18
$$\mathrm{great}\:\mathrm{work} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 25/Dec/18
![(a+b)^6 =a^6 +6c_1 a^5 b+6c_2 a^4 b^2 +6c_3 a^3 b^3 +6c_4 a^2 b^4 +6c_5 ab^5 +b^6 (a−b)^6 =a^6 −6c_1 a^5 b+6c_2 a^4 b^2 −6c_3 a^3 b^3 +6c_4 a^2 b^4 −6c_5 ab^5 +b^6 (a+b)^6 −(a−b)^6 =2[6c_1 a^5 b+6c_3 a^3 b^3 +6c_5 ab^5 ] =2[6a^5 b+20a^3 b^3 +6ab^5 ] =12((√5) )^5 (2)+40((√5) )^3 (2)^3 +12((√5) )(2)^5 =12×2×25×(√5) +40×8×5(√5) +32×12×(√5) =8(√5) (75+200+48) ans is 75+200+48=323](https://www.tinkutara.com/question/Q51246.png)
$$\left({a}+{b}\right)^{\mathrm{6}} ={a}^{\mathrm{6}} +\mathrm{6}{c}_{\mathrm{1}} {a}^{\mathrm{5}} {b}+\mathrm{6}{c}_{\mathrm{2}} {a}^{\mathrm{4}} {b}^{\mathrm{2}} +\mathrm{6}{c}_{\mathrm{3}} {a}^{\mathrm{3}} {b}^{\mathrm{3}} +\mathrm{6}{c}_{\mathrm{4}} {a}^{\mathrm{2}} {b}^{\mathrm{4}} +\mathrm{6}{c}_{\mathrm{5}} {ab}^{\mathrm{5}} +{b}^{\mathrm{6}} \\ $$$$\left({a}−{b}\right)^{\mathrm{6}} ={a}^{\mathrm{6}} −\mathrm{6}{c}_{\mathrm{1}} {a}^{\mathrm{5}} {b}+\mathrm{6}{c}_{\mathrm{2}} {a}^{\mathrm{4}} {b}^{\mathrm{2}} −\mathrm{6}{c}_{\mathrm{3}} {a}^{\mathrm{3}} {b}^{\mathrm{3}} +\mathrm{6}{c}_{\mathrm{4}} {a}^{\mathrm{2}} {b}^{\mathrm{4}} −\mathrm{6}{c}_{\mathrm{5}} {ab}^{\mathrm{5}} +{b}^{\mathrm{6}} \\ $$$$\left({a}+{b}\right)^{\mathrm{6}} −\left({a}−{b}\right)^{\mathrm{6}} \\ $$$$=\mathrm{2}\left[\mathrm{6}{c}_{\mathrm{1}} {a}^{\mathrm{5}} {b}+\mathrm{6}{c}_{\mathrm{3}} {a}^{\mathrm{3}} {b}^{\mathrm{3}} +\mathrm{6}{c}_{\mathrm{5}} {ab}^{\mathrm{5}} \right] \\ $$$$=\mathrm{2}\left[\mathrm{6}{a}^{\mathrm{5}} {b}+\mathrm{20}{a}^{\mathrm{3}} {b}^{\mathrm{3}} +\mathrm{6}{ab}^{\mathrm{5}} \right] \\ $$$$=\mathrm{12}\left(\sqrt{\mathrm{5}}\:\right)^{\mathrm{5}} \left(\mathrm{2}\right)+\mathrm{40}\left(\sqrt{\mathrm{5}}\:\right)^{\mathrm{3}} \left(\mathrm{2}\right)^{\mathrm{3}} +\mathrm{12}\left(\sqrt{\mathrm{5}}\:\right)\left(\mathrm{2}\right)^{\mathrm{5}} \\ $$$$=\mathrm{12}×\mathrm{2}×\mathrm{25}×\sqrt{\mathrm{5}}\:+\mathrm{40}×\mathrm{8}×\mathrm{5}\sqrt{\mathrm{5}}\:+\mathrm{32}×\mathrm{12}×\sqrt{\mathrm{5}}\: \\ $$$$=\mathrm{8}\sqrt{\mathrm{5}}\:\left(\mathrm{75}+\mathrm{200}+\mathrm{48}\right) \\ $$$${ans}\:{is}\:\mathrm{75}+\mathrm{200}+\mathrm{48}=\mathrm{323} \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$ \\ $$
Commented by peter frank last updated on 25/Dec/18
$${perfect}\:{sir}.{binomial}\:{expansion}\: \\ $$$${i}\:{hesitate}\:{to}\:{apply}\:{that}\: \\ $$$${method} \\ $$