Question Number 60725 by naka3546 last updated on 25/May/19
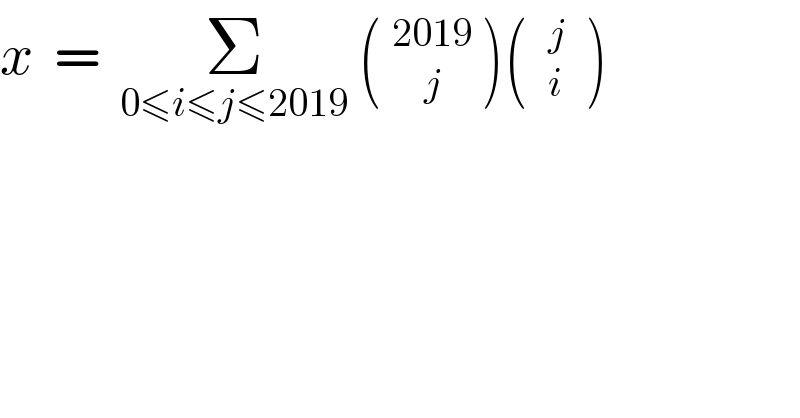
$${x}\:\:=\:\:\underset{\mathrm{0}\leqslant{i}\leqslant{j}\leqslant\mathrm{2019}} {\sum}\:\left(\:_{\:\:\:\:{j}} ^{\mathrm{2019}} \:\right)\left(\:\:_{{i}} ^{{j}} \:\:\right)\: \\ $$
Commented by naka3546 last updated on 25/May/19

$${x}\:\:=\:\:? \\ $$
Commented by Mr X pcx last updated on 25/May/19
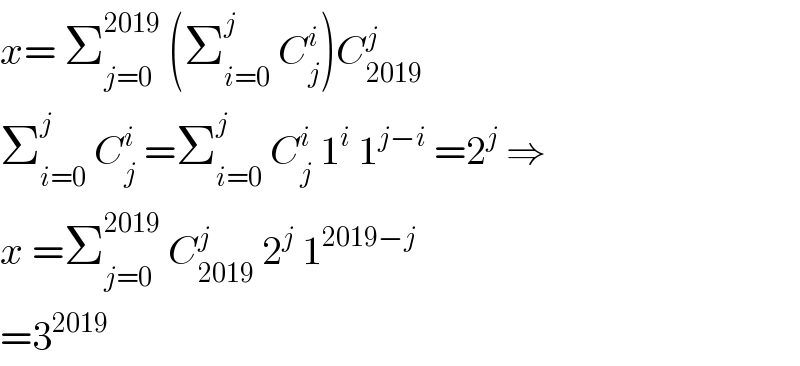
$${x}=\:\sum_{{j}=\mathrm{0}} ^{\mathrm{2019}} \:\left(\sum_{{i}=\mathrm{0}} ^{{j}} \:{C}_{{j}} ^{{i}} \right){C}_{\mathrm{2019}} ^{{j}} \\ $$$$\sum_{{i}=\mathrm{0}} ^{{j}} \:{C}_{{j}} ^{{i}} \:=\sum_{{i}=\mathrm{0}} ^{{j}} \:{C}_{{j}} ^{{i}} \:\mathrm{1}^{{i}} \:\mathrm{1}^{{j}−{i}} \:=\mathrm{2}^{{j}} \:\Rightarrow \\ $$$${x}\:=\sum_{{j}=\mathrm{0}} ^{\mathrm{2019}} \:{C}_{\mathrm{2019}} ^{{j}} \:\mathrm{2}^{{j}} \:\mathrm{1}^{\mathrm{2019}−{j}} \\ $$$$=\mathrm{3}^{\mathrm{2019}} \\ $$
