x-0-pi-2-sinx-cosx-tg3x-

Question Number 60587 by behi83417@gmail.com last updated on 22/May/19

x \in [0, \frac{π}{2}]

sinx + cosx = tg 3 x

Commented by MJS last updated on 22/May/19

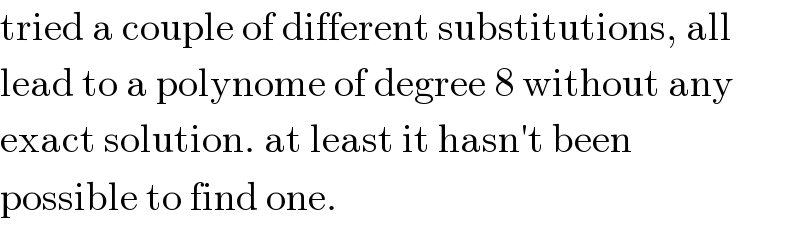
tried a couple of different substitutions, all

lead to a polynome of degree 8 without any

exact solution . at least it {hasn}^{'} t been

possible to find one .

Answered by ajfour last updated on 22/May/19

let \tan \frac{x}{2} = t, then

\frac{2 t}{1 + t^{2}} + \frac{1 - t^{2}}{1 + t^{2}} = \frac{\frac{6 t}{1 - t^{2}} - {(\frac{2 t}{1 - t^{2}})}^{3}}{1 - 3 {(\frac{2 t}{1 - t^{2}})}^{2}}

\Rightarrow \frac{(2 t + 1 - t^{2})}{1 + t^{2}} = \frac{6 t {(1 - t^{2})}^{2} - {8 t}^{3}}{{(1 - t^{2})}^{3} - {12 t}^{2} (1 - t^{2})}

\Rightarrow \frac{2 t + 1 - t^{2}}{1 + t^{2}} = \frac{2 t ({3 t}^{4} - {10 t}^{2} + 3)}{(1 - t^{2}) (1 - {14 t}^{2} + t^{4})}

\Rightarrow (2 t + 1 - t^{2}) (1 - t^{2}) (1 - {14 t}^{2} + t^{4})

= 2 t (1 + t^{2}) ({3 t}^{4} - {10 t}^{2} + 3)

\dots .

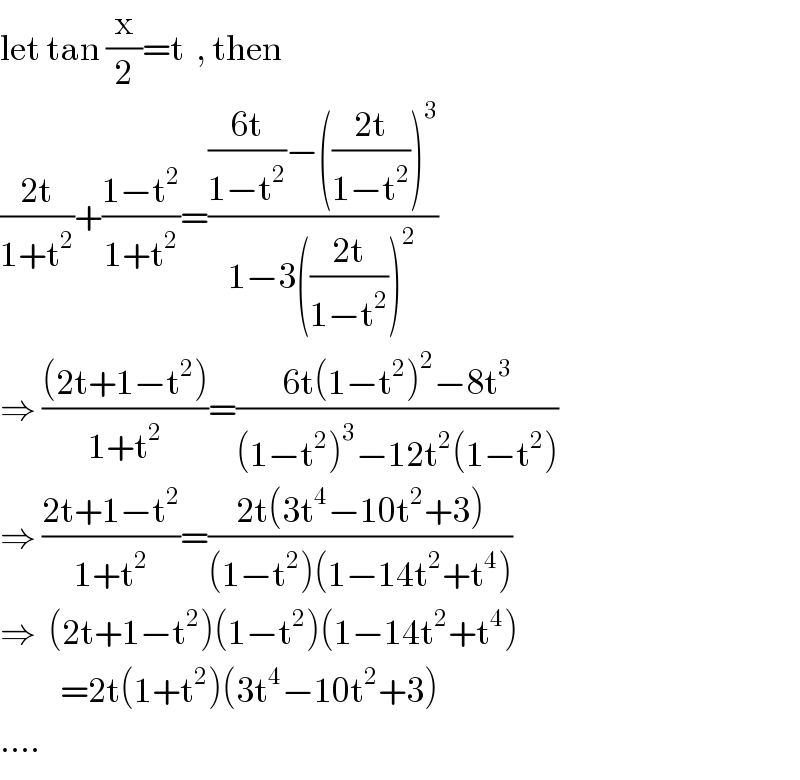
Answered by tanmay last updated on 22/May/19

t r y i n g \dots

w h e n x \in [0, \frac{π}{2}] s i n x \in [0, 1]

w h e n x \in [0, \frac{π}{2}] c o s x \in [0, 1]

s i n x + c o s x

\sqrt{2} (\frac{1}{\sqrt{2}} s i n x + \frac{1}{\sqrt{2}} c o s x)

= \sqrt{2} s i n (\frac{π}{4} + x)

s o w h e n x \in [0, \frac{π}{2}] (s i n x + c o s x) \in [1, 1.41]

\frac{x}{3 x} \frac{10^{o}}{30^{o}} \frac{20^{o}}{60^{o}} \frac{30^{o}}{90^{o}} \frac{40^{o}}{120^{o}} \frac{50^{o}}{150^{0}} \frac{60^{o}}{180^{o}} \frac{70^{o}}{210^{o}} \frac{80^{o}}{240^{o}} \frac{90^{l}}{270^{o}}

w h e n x = 10^{o} t a n 3 x \approx 0.58

w h e n x = 20^{o} t a n 3 x \approx 1.73

s o w h e n x \in [10^{o}, 20^{o}] t a n 3 x = (s i n x + c o s x)

(1) s o o n e r o o t l i e w h e n x \in [\frac{π}{18}, \frac{2 π}{18}]

w h e n 60^{o} ⩾ x > 30^{o}

180^{o} ⩾ 3 x > 90^{o} v a l u e o f t a n 3 x (- v e)

s i n c e a n g l e l i e i n s e c o n d q u a d r a n t .

b u t (s i n x + c o s x) \in [1, 1.41]

(2) s o n o r o o t l i e w h e n x \in [\frac{3 π}{18}, \frac{6 π}{18}]

x = 70^{o} t a n 3 x \approx 0.58

x = 80^{o} t a n 3 x \approx 1.73

s o o n e r o o t l i e w h e n x \in [\frac{7 π}{18}, \frac{8 π}{18}]

s o g i v e n e q u a t i o n h a s t w o r o o t i n

x \in [0, \frac{π}{2}]

p l s c h e c k \dots

Commented by tanmay last updated on 22/May/19

m o s t w e l c o m e s i r

Commented by behi83417@gmail.com last updated on 22/May/19

t h a k s i n a d v a n c e a l l m y b e s t f r i e n d s .

s i r t a n m a y! i t h i n k y o u a r e r i g h t .