Question Number 89920 by akash4081 last updated on 20/Apr/20
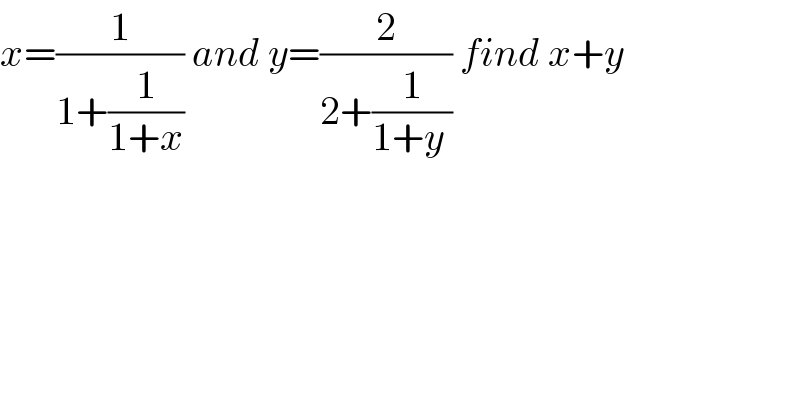
$${x}=\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}+{x}}}\:{and}\:{y}=\frac{\mathrm{2}}{\mathrm{2}+\frac{\mathrm{1}}{\mathrm{1}+{y}\:}}\:{find}\:{x}+{y} \\ $$
Commented by john santu last updated on 20/Apr/20

$${x}\:=\:\frac{{x}+\mathrm{1}}{{x}+\mathrm{2}}\:\Rightarrow\:{x}\:=\:\frac{−\mathrm{1}\:\pm\:\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$${y}\:=\:\frac{\mathrm{2}\left({y}+\mathrm{1}\right)}{\mathrm{2}{y}+\mathrm{3}}\:\Rightarrow\:{y}\:=\:\frac{−\mathrm{1}\:\pm\:\sqrt{\mathrm{17}}}{\mathrm{4}} \\ $$$$\therefore\:{x}+{y}\:=\:\left(\frac{−\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{2}}\right)+\left(\frac{−\mathrm{1}\pm\sqrt{\mathrm{17}}}{\mathrm{4}}\right) \\ $$
