Menu Close

x-1-1-x-1-1-dx-

Tinku Tara 0 Comments
Pin




Question Number 85596 by M±th+et£s last updated on 23/Mar/20
∫(((√(x+1))−1)/( (√(x−1))+1)) dx
$$\int\frac{\sqrt{{x}+\mathrm{1}}−\mathrm{1}}{\:\sqrt{{x}−\mathrm{1}}+\mathrm{1}}\:{dx} \\ $$
Commented by mathmax by abdo last updated on 23/Mar/20
A =∫ (((√(x+1))−1)/( (√(x−1))+1))dx chagement (√(x−1))+1 =t give (√(x−1))=t−1 ⇒ x−1 =(t−1)^2 ⇒dx =2(t−1)dt ⇒ A =∫(((√(1+(t−1)^2 ))−1)/t)2(t−1)dt =2 ∫ ((t−1)/t)(√((t−1)^2 +1))dt =2 ∫(1−(1/t))(√((t−1)^2 +1))dt =2∫(√((t−1)^2 +1))dt−2 ∫ ((√((t−1)^2 +1))/t)dt ∫ (√(1+(t−1)^2 ))dt =_(t−1=sh(u)) ∫ ch^2 (u)du =(1/2)∫ (1+ch(2u))du =(u/2) +(1/4)sh(2u) +c_1 =(u/2) +(1/2)sh(u)ch(u) +c_1 =(1/2)ln(t−1 +(√(1+(t−1)^2 ))) +(1/2)(t−1)(√(1+(t−1)^2 ))+c_1 =(1/2)ln((√(x−1))+(√(1+x−1))) +(1/2)(√(x−1))(√(1+x−1))+c_1 =(1/2)ln((√(x−1))+(√x))+(1/2)(√(x−1))(√x) +c_1 ∫ ((√(1+(t−1)^2 ))/t)dt =_(t−1=sh(u)) ∫ ((chu)/(1+sh(u)))ch(u)du =(1/2)∫ (((1+ch(2u)))/(1+sh(u)))du =(1/2)∫ (((1+((e^(2u) +e^(−2u) )/2)))/(1+((e^u −e^(−u) )/2)))du =(1/2)∫ ((2 +e^(2u) +e^(−2u) )/(2+e^u −e^(−u) ))du =(1/2)∫ ((2e^(2u) +e^(4u) +1)/(2e^(2u) +e^(3u) −e^u ))du =_(e^u =z) (1/2)∫ ((z^4 +2z^2 +1)/(z^3 +2z^2 −z)) (dz/z) =(1/2)∫ ((z^4 +2z^2 +1)/(z^4 +2z^3 −z^2 ))dz =(1/2)∫ ((z^4 +2z^3 −z^2 +2z^2 +1−2z^3 +z^2 )/(z^4 +2z^3 −z^2 ))dz =(1/2)∫dz +(1/2)∫ ((−2z^3 +3z^2 +1)/(z^4 +2z^3 −z^2 ))dz let decompose F(z) =((−2z^3 +3z^2 +1)/(z^2 (z^2 +2z−1))) ⇒F(z)=((−2z^3 +3z^2 +1)/(z^2 ((z+1)^2 −2))) =((−2z^3 +3z^2 +1)/(z^2 (z+1−(√2))(z+1+(√2)))) =(a/z) +(b/z^2 ) +(c/(z+1−(√2))) +(d/(z+1+(√2))) ⇒∫ F(z)dz =aln∣z∣ −(b/z) +cln∣z+1−(√2)∣+dln∣z+1+(√2)∣ +C rest calculus of coefgicients...be continued..
$${A}\:=\int\:\:\frac{\sqrt{{x}+\mathrm{1}}−\mathrm{1}}{\:\sqrt{{x}−\mathrm{1}}+\mathrm{1}}{dx}\:\:\:\:{chagement}\:\sqrt{{x}−\mathrm{1}}+\mathrm{1}\:={t}\:{give}\:\sqrt{{x}−\mathrm{1}}={t}−\mathrm{1}\:\Rightarrow \\ $$$${x}−\mathrm{1}\:=\left({t}−\mathrm{1}\right)^{\mathrm{2}} \:\Rightarrow{dx}\:=\mathrm{2}\left({t}−\mathrm{1}\right){dt}\:\Rightarrow \\ $$$${A}\:=\int\frac{\sqrt{\mathrm{1}+\left({t}−\mathrm{1}\right)^{\mathrm{2}} }−\mathrm{1}}{{t}}\mathrm{2}\left({t}−\mathrm{1}\right){dt}\:=\mathrm{2}\:\int\:\frac{{t}−\mathrm{1}}{{t}}\sqrt{\left({t}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}}{dt} \\ $$$$=\mathrm{2}\:\int\left(\mathrm{1}−\frac{\mathrm{1}}{{t}}\right)\sqrt{\left({t}−\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{1}}{dt}\:=\mathrm{2}\int\sqrt{\left({t}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}}{dt}−\mathrm{2}\:\int\:\:\frac{\sqrt{\left({t}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}}}{{t}}{dt} \\ $$$$\int\:\sqrt{\mathrm{1}+\left({t}−\mathrm{1}\right)^{\mathrm{2}} }{dt}\:=_{{t}−\mathrm{1}={sh}\left({u}\right)} \:\:\int\:{ch}^{\mathrm{2}} \left({u}\right){du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\:\left(\mathrm{1}+{ch}\left(\mathrm{2}{u}\right)\right){du}\:=\frac{{u}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{4}}{sh}\left(\mathrm{2}{u}\right)\:+{c}_{\mathrm{1}} \\ $$$$=\frac{{u}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}}{sh}\left({u}\right){ch}\left({u}\right)\:+{c}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({t}−\mathrm{1}\:+\sqrt{\mathrm{1}+\left({t}−\mathrm{1}\right)^{\mathrm{2}} }\right) \\ $$$$+\frac{\mathrm{1}}{\mathrm{2}}\left({t}−\mathrm{1}\right)\sqrt{\mathrm{1}+\left({t}−\mathrm{1}\right)^{\mathrm{2}} }+{c}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\sqrt{{x}−\mathrm{1}}+\sqrt{\mathrm{1}+{x}−\mathrm{1}}\right) \\ $$$$+\frac{\mathrm{1}}{\mathrm{2}}\sqrt{{x}−\mathrm{1}}\sqrt{\mathrm{1}+{x}−\mathrm{1}}+{c}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\sqrt{{x}−\mathrm{1}}+\sqrt{{x}}\right)+\frac{\mathrm{1}}{\mathrm{2}}\sqrt{{x}−\mathrm{1}}\sqrt{{x}}\:+{c}_{\mathrm{1}} \\ $$$$\int\:\frac{\sqrt{\mathrm{1}+\left({t}−\mathrm{1}\right)^{\mathrm{2}} }}{{t}}{dt}\:=_{{t}−\mathrm{1}={sh}\left({u}\right)} \:\:\:\:\int\:\:\frac{{chu}}{\mathrm{1}+{sh}\left({u}\right)}{ch}\left({u}\right){du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\frac{\left(\mathrm{1}+{ch}\left(\mathrm{2}{u}\right)\right)}{\mathrm{1}+{sh}\left({u}\right)}{du}\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\frac{\left(\mathrm{1}+\frac{{e}^{\mathrm{2}{u}} \:+{e}^{−\mathrm{2}{u}} }{\mathrm{2}}\right)}{\mathrm{1}+\frac{{e}^{{u}} −{e}^{−{u}} }{\mathrm{2}}}{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\frac{\mathrm{2}\:+{e}^{\mathrm{2}{u}} +{e}^{−\mathrm{2}{u}} }{\mathrm{2}+{e}^{{u}} −{e}^{−{u}} }{du}\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\frac{\mathrm{2}{e}^{\mathrm{2}{u}} +{e}^{\mathrm{4}{u}} +\mathrm{1}}{\mathrm{2}{e}^{\mathrm{2}{u}} \:+{e}^{\mathrm{3}{u}} −{e}^{{u}} }{du} \\ $$$$=_{{e}^{{u}} ={z}} \:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\frac{{z}^{\mathrm{4}} \:+\mathrm{2}{z}^{\mathrm{2}} \:+\mathrm{1}}{{z}^{\mathrm{3}} \:+\mathrm{2}{z}^{\mathrm{2}} −{z}}\:\frac{{dz}}{{z}}\:=\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\:\frac{{z}^{\mathrm{4}} \:+\mathrm{2}{z}^{\mathrm{2}} \:+\mathrm{1}}{{z}^{\mathrm{4}} \:+\mathrm{2}{z}^{\mathrm{3}} −{z}^{\mathrm{2}} }{dz} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\frac{{z}^{\mathrm{4}} \:+\mathrm{2}{z}^{\mathrm{3}} −{z}^{\mathrm{2}} \:+\mathrm{2}{z}^{\mathrm{2}} \:+\mathrm{1}−\mathrm{2}{z}^{\mathrm{3}} +{z}^{\mathrm{2}} \:}{{z}^{\mathrm{4}} +\mathrm{2}{z}^{\mathrm{3}} \:−{z}^{\mathrm{2}} }{dz} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int{dz}\:+\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{−\mathrm{2}{z}^{\mathrm{3}} +\mathrm{3}{z}^{\mathrm{2}} \:+\mathrm{1}}{{z}^{\mathrm{4}} +\mathrm{2}{z}^{\mathrm{3}} −{z}^{\mathrm{2}} }{dz}\:{let}\:{decompose}\: \\ $$$${F}\left({z}\right)\:=\frac{−\mathrm{2}{z}^{\mathrm{3}} \:+\mathrm{3}{z}^{\mathrm{2}} +\mathrm{1}}{{z}^{\mathrm{2}} \left({z}^{\mathrm{2}} \:+\mathrm{2}{z}−\mathrm{1}\right)}\:\Rightarrow{F}\left({z}\right)=\frac{−\mathrm{2}{z}^{\mathrm{3}} \:+\mathrm{3}{z}^{\mathrm{2}} \:+\mathrm{1}}{{z}^{\mathrm{2}} \left(\left({z}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}\right)} \\ $$$$=\frac{−\mathrm{2}{z}^{\mathrm{3}} \:+\mathrm{3}{z}^{\mathrm{2}} \:+\mathrm{1}}{{z}^{\mathrm{2}} \left({z}+\mathrm{1}−\sqrt{\mathrm{2}}\right)\left({z}+\mathrm{1}+\sqrt{\mathrm{2}}\right)}\:=\frac{{a}}{{z}}\:+\frac{{b}}{{z}^{\mathrm{2}} }\:+\frac{{c}}{{z}+\mathrm{1}−\sqrt{\mathrm{2}}}\:+\frac{{d}}{{z}+\mathrm{1}+\sqrt{\mathrm{2}}} \\ $$$$\Rightarrow\int\:{F}\left({z}\right){dz}\:={aln}\mid{z}\mid\:−\frac{{b}}{{z}}\:+{cln}\mid{z}+\mathrm{1}−\sqrt{\mathrm{2}}\mid+{dln}\mid{z}+\mathrm{1}+\sqrt{\mathrm{2}}\mid\:+{C} \\ $$$${rest}\:{calculus}\:{of}\:{coefgicients}…{be}\:{continued}.. \\ $$
Answered by MJS last updated on 23/Mar/20
∫(((√(x+1))−1)/( (√(x−1))+1))dx= [t=(√(x−1)) → dx=2(√(x−1))dt] =2∫((t(√(t^2 +2))−t)/(t+1))dt= =−2∫((√(t^2 +2))/(t+1))dt+2∫(√(t^2 +2))dt+2∫(dt/(t+1))−2∫dt −2∫dt=−2t=−2(√(x−1)) • 2∫(dt/(t+1))=2ln (t+1) =2ln ((√(x−1))+1) • 2∫(√(t^2 +2))dt=t(√(t^2 +2))+2ln (t+(√(t^2 +2))) = =(√(x−1))(√(x+1))+2ln ((√(x−1))+(√(x+1))) • −2∫((√(t^2 +2))/(t+1))dt= I prefer t=(√2)sinh (ln u) to avoid another step [u=((t+(√(t^2 +2)))/( (√2))) → dt=((√(2(t^2 +2)))/(t+(√t^2 )+2))du=((u^2 +1)/( (√2)u^2 ))du] =−(√2)∫(((u^2 +1)^2 )/(u^2 (u^2 +(√2)u−1)))du= =−(√2)∫(((u^2 +1)^2 )/(u^2 (u+(((√2)+(√6))/2))(u+(((√2)−(√6))/2))))du= =2(√3)∫(du/(u+(((√2)+(√6))/2)))−2(√3)∫(du/(u+(((√2)−(√6))/2)))+2∫(du/u)+(√2)∫(du/u^2 )−(√2)∫du= =2(√3)ln (u+(((√2)+(√6))/2)) −2(√3)ln (u+(((√2)−(√6))/2)) +2ln u −((√2)/u)−(√2)u= =2(√3)ln ((2u+(√2)+(√6))/(2u+(√2)−(√6))) +2ln u −(((√2)(u^2 +1))/u)= =2(√3)ln ((2((√(x−1))+(√(x+1)))+(√2)+(√6))/(2((√(x−1))+(√(x+1)))+(√2)−(√6)))+2ln ((√(x−1))+(√(x+1))) −2(√(x+1)) • ⇒ ∫(((√(x+1))−1)/( (√(x−1))+1))dx=the sum of the marked terms • please check for typos
$$\int\frac{\sqrt{{x}+\mathrm{1}}−\mathrm{1}}{\:\sqrt{{x}−\mathrm{1}}+\mathrm{1}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\sqrt{{x}−\mathrm{1}}\:\rightarrow\:{dx}=\mathrm{2}\sqrt{{x}−\mathrm{1}}{dt}\right] \\ $$$$=\mathrm{2}\int\frac{{t}\sqrt{{t}^{\mathrm{2}} +\mathrm{2}}−{t}}{{t}+\mathrm{1}}{dt}= \\ $$$$=−\mathrm{2}\int\frac{\sqrt{{t}^{\mathrm{2}} +\mathrm{2}}}{{t}+\mathrm{1}}{dt}+\mathrm{2}\int\sqrt{{t}^{\mathrm{2}} +\mathrm{2}}{dt}+\mathrm{2}\int\frac{{dt}}{{t}+\mathrm{1}}−\mathrm{2}\int{dt} \\ $$$$ \\ $$$$−\mathrm{2}\int{dt}=−\mathrm{2}{t}=−\mathrm{2}\sqrt{{x}−\mathrm{1}}\:\bullet \\ $$$$\mathrm{2}\int\frac{{dt}}{{t}+\mathrm{1}}=\mathrm{2ln}\:\left({t}+\mathrm{1}\right)\:=\mathrm{2ln}\:\left(\sqrt{{x}−\mathrm{1}}+\mathrm{1}\right)\:\bullet \\ $$$$\mathrm{2}\int\sqrt{{t}^{\mathrm{2}} +\mathrm{2}}{dt}={t}\sqrt{{t}^{\mathrm{2}} +\mathrm{2}}+\mathrm{2ln}\:\left({t}+\sqrt{{t}^{\mathrm{2}} +\mathrm{2}}\right)\:= \\ $$$$\:\:\:\:\:=\sqrt{{x}−\mathrm{1}}\sqrt{{x}+\mathrm{1}}+\mathrm{2ln}\:\left(\sqrt{{x}−\mathrm{1}}+\sqrt{{x}+\mathrm{1}}\right)\:\bullet \\ $$$$ \\ $$$$−\mathrm{2}\int\frac{\sqrt{{t}^{\mathrm{2}} +\mathrm{2}}}{{t}+\mathrm{1}}{dt}= \\ $$$$\:\:\:\:\:\mathrm{I}\:\mathrm{prefer}\:{t}=\sqrt{\mathrm{2}}\mathrm{sinh}\:\left(\mathrm{ln}\:{u}\right)\:\mathrm{to}\:\mathrm{avoid}\:\mathrm{another}\:\mathrm{step} \\ $$$$\:\:\:\:\:\left[{u}=\frac{{t}+\sqrt{{t}^{\mathrm{2}} +\mathrm{2}}}{\:\sqrt{\mathrm{2}}}\:\rightarrow\:{dt}=\frac{\sqrt{\mathrm{2}\left({t}^{\mathrm{2}} +\mathrm{2}\right)}}{{t}+\sqrt{{t}^{\mathrm{2}} }+\mathrm{2}}{du}=\frac{{u}^{\mathrm{2}} +\mathrm{1}}{\:\sqrt{\mathrm{2}}{u}^{\mathrm{2}} }{du}\right] \\ $$$$=−\sqrt{\mathrm{2}}\int\frac{\left({u}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{{u}^{\mathrm{2}} \left({u}^{\mathrm{2}} +\sqrt{\mathrm{2}}{u}−\mathrm{1}\right)}{du}= \\ $$$$=−\sqrt{\mathrm{2}}\int\frac{\left({u}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{{u}^{\mathrm{2}} \left({u}+\frac{\sqrt{\mathrm{2}}+\sqrt{\mathrm{6}}}{\mathrm{2}}\right)\left({u}+\frac{\sqrt{\mathrm{2}}−\sqrt{\mathrm{6}}}{\mathrm{2}}\right)}{du}= \\ $$$$=\mathrm{2}\sqrt{\mathrm{3}}\int\frac{{du}}{{u}+\frac{\sqrt{\mathrm{2}}+\sqrt{\mathrm{6}}}{\mathrm{2}}}−\mathrm{2}\sqrt{\mathrm{3}}\int\frac{{du}}{{u}+\frac{\sqrt{\mathrm{2}}−\sqrt{\mathrm{6}}}{\mathrm{2}}}+\mathrm{2}\int\frac{{du}}{{u}}+\sqrt{\mathrm{2}}\int\frac{{du}}{{u}^{\mathrm{2}} }−\sqrt{\mathrm{2}}\int{du}= \\ $$$$=\mathrm{2}\sqrt{\mathrm{3}}\mathrm{ln}\:\left({u}+\frac{\sqrt{\mathrm{2}}+\sqrt{\mathrm{6}}}{\mathrm{2}}\right)\:−\mathrm{2}\sqrt{\mathrm{3}}\mathrm{ln}\:\left({u}+\frac{\sqrt{\mathrm{2}}−\sqrt{\mathrm{6}}}{\mathrm{2}}\right)\:+\mathrm{2ln}\:{u}\:−\frac{\sqrt{\mathrm{2}}}{{u}}−\sqrt{\mathrm{2}}{u}= \\ $$$$=\mathrm{2}\sqrt{\mathrm{3}}\mathrm{ln}\:\frac{\mathrm{2}{u}+\sqrt{\mathrm{2}}+\sqrt{\mathrm{6}}}{\mathrm{2}{u}+\sqrt{\mathrm{2}}−\sqrt{\mathrm{6}}}\:+\mathrm{2ln}\:{u}\:−\frac{\sqrt{\mathrm{2}}\left({u}^{\mathrm{2}} +\mathrm{1}\right)}{{u}}= \\ $$$$=\mathrm{2}\sqrt{\mathrm{3}}\mathrm{ln}\:\frac{\mathrm{2}\left(\sqrt{{x}−\mathrm{1}}+\sqrt{{x}+\mathrm{1}}\right)+\sqrt{\mathrm{2}}+\sqrt{\mathrm{6}}}{\mathrm{2}\left(\sqrt{{x}−\mathrm{1}}+\sqrt{{x}+\mathrm{1}}\right)+\sqrt{\mathrm{2}}−\sqrt{\mathrm{6}}}+\mathrm{2ln}\:\left(\sqrt{{x}−\mathrm{1}}+\sqrt{{x}+\mathrm{1}}\right)\:−\mathrm{2}\sqrt{{x}+\mathrm{1}}\:\bullet \\ $$$$ \\ $$$$\Rightarrow \\ $$$$\int\frac{\sqrt{{x}+\mathrm{1}}−\mathrm{1}}{\:\sqrt{{x}−\mathrm{1}}+\mathrm{1}}{dx}=\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{marked}\:\mathrm{terms}\:\bullet \\ $$$$\mathrm{please}\:\mathrm{check}\:\mathrm{for}\:\mathrm{typos} \\ $$
Commented by M±th+et£s last updated on 23/Mar/20
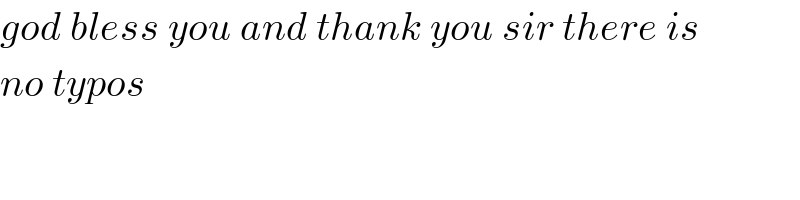
god bless you and thank you sir there is no typos
$${god}\:{bless}\:{you}\:{and}\:{thank}\:{you}\:{sir}\:{there}\:{is} \\ $$$${no}\:{typos}\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *