Question Number 182575 by CrispyXYZ last updated on 11/Dec/22
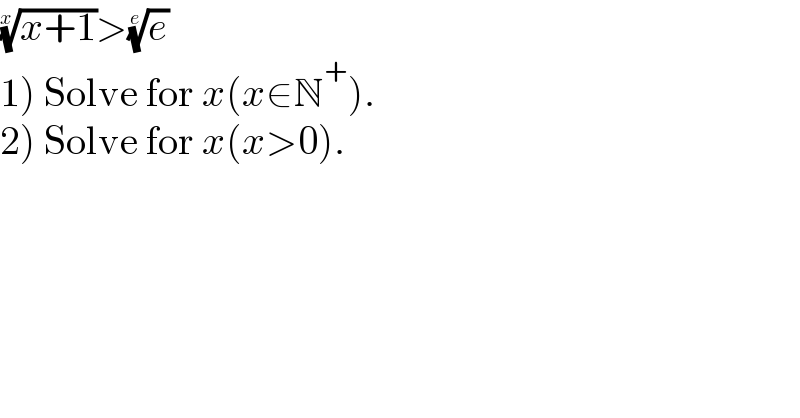
$$\sqrt[{{x}}]{{x}+\mathrm{1}}>\sqrt[{{e}}]{{e}} \\ $$$$\left.\mathrm{1}\right)\:\mathrm{Solve}\:\mathrm{for}\:{x}\left({x}\in\mathbb{N}^{+} \right). \\ $$$$\left.\mathrm{2}\right)\:\mathrm{Solve}\:\mathrm{for}\:{x}\left({x}>\mathrm{0}\right). \\ $$
Answered by mr W last updated on 12/Dec/22
![f(x)=(1+x)^(1/x) for x>0: f(x) is strictly decreasing. f(x)=(1+x)^(1/x) =e^(1/e) ⇒x_1 ≈4.7591 (solution see later) (1+x)^(1/x) >e^(1/e) ⇒0<x<x_1 ≈4.7591 1) x∈[1,4] 2) x∈(0,4.7591)](https://www.tinkutara.com/question/Q182630.png)
$${f}\left({x}\right)=\left(\mathrm{1}+{x}\right)^{\frac{\mathrm{1}}{{x}}} \\ $$$${for}\:{x}>\mathrm{0}: \\ $$$${f}\left({x}\right)\:{is}\:{strictly}\:{decreasing}. \\ $$$${f}\left({x}\right)=\left(\mathrm{1}+{x}\right)^{\frac{\mathrm{1}}{{x}}} ={e}^{\frac{\mathrm{1}}{{e}}} \:\Rightarrow{x}_{\mathrm{1}} \approx\mathrm{4}.\mathrm{7591}\:\left({solution}\:{see}\:{later}\right) \\ $$$$\left(\mathrm{1}+{x}\right)^{\frac{\mathrm{1}}{{x}}} >{e}^{\frac{\mathrm{1}}{{e}}} \\ $$$$\:\Rightarrow\mathrm{0}<{x}<{x}_{\mathrm{1}} \approx\mathrm{4}.\mathrm{7591} \\ $$$$\left.\mathrm{1}\right)\:{x}\in\left[\mathrm{1},\mathrm{4}\right] \\ $$$$\left.\mathrm{2}\right)\:{x}\in\left(\mathrm{0},\mathrm{4}.\mathrm{7591}\right) \\ $$
Commented by mr W last updated on 12/Dec/22
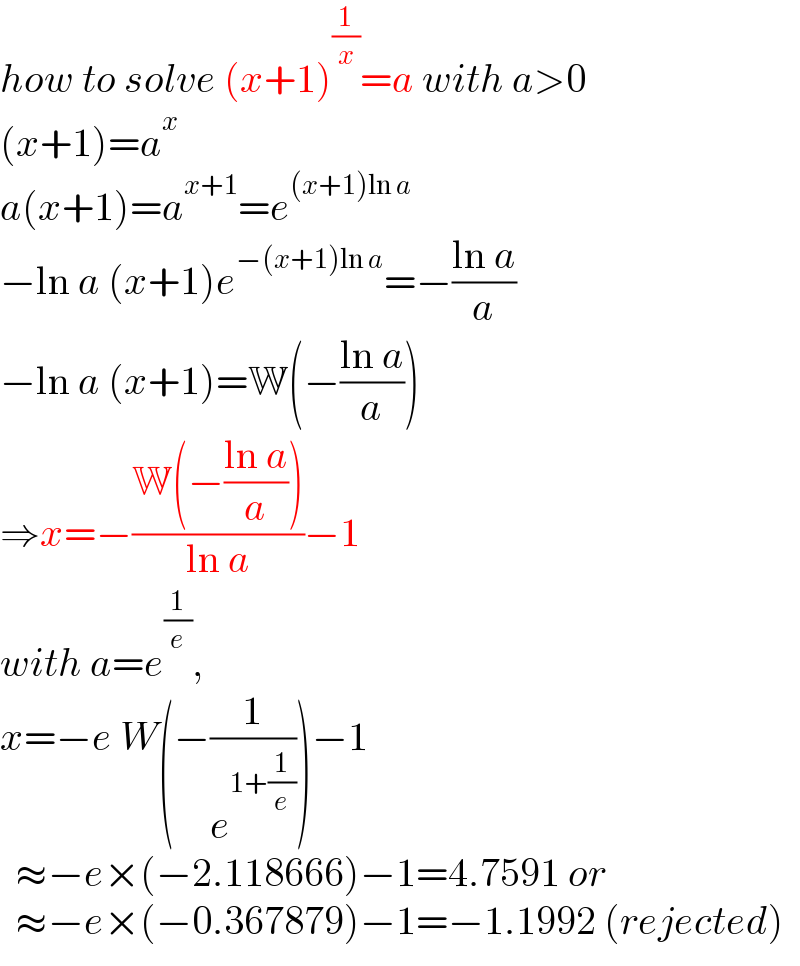
$${how}\:{to}\:{solve}\:\left({x}+\mathrm{1}\right)^{\frac{\mathrm{1}}{{x}}} ={a}\:{with}\:{a}>\mathrm{0} \\ $$$$\left({x}+\mathrm{1}\right)={a}^{{x}} \\ $$$${a}\left({x}+\mathrm{1}\right)={a}^{{x}+\mathrm{1}} ={e}^{\left({x}+\mathrm{1}\right)\mathrm{ln}\:{a}} \\ $$$$−\mathrm{ln}\:{a}\:\left({x}+\mathrm{1}\right){e}^{−\left({x}+\mathrm{1}\right)\mathrm{ln}\:{a}} =−\frac{\mathrm{ln}\:{a}}{{a}} \\ $$$$−\mathrm{ln}\:{a}\:\left({x}+\mathrm{1}\right)=\mathbb{W}\left(−\frac{\mathrm{ln}\:{a}}{{a}}\right) \\ $$$$\Rightarrow{x}=−\frac{\mathbb{W}\left(−\frac{\mathrm{ln}\:{a}}{{a}}\right)}{\mathrm{ln}\:{a}}−\mathrm{1} \\ $$$${with}\:{a}={e}^{\frac{\mathrm{1}}{{e}}} , \\ $$$${x}=−{e}\:{W}\left(−\frac{\mathrm{1}}{{e}^{\mathrm{1}+\frac{\mathrm{1}}{{e}}} }\right)−\mathrm{1} \\ $$$$\:\:\approx−{e}×\left(−\mathrm{2}.\mathrm{118666}\right)−\mathrm{1}=\mathrm{4}.\mathrm{7591}\:{or} \\ $$$$\:\:\approx−{e}×\left(−\mathrm{0}.\mathrm{367879}\right)−\mathrm{1}=−\mathrm{1}.\mathrm{1992}\:\left({rejected}\right) \\ $$
