Menu Close

x-1-2-y-1-2-27xy-x-2-1-y-2-1-10xy-

Tinku Tara 0 Comments
Pin




Question Number 88811 by jagoll last updated on 13/Apr/20
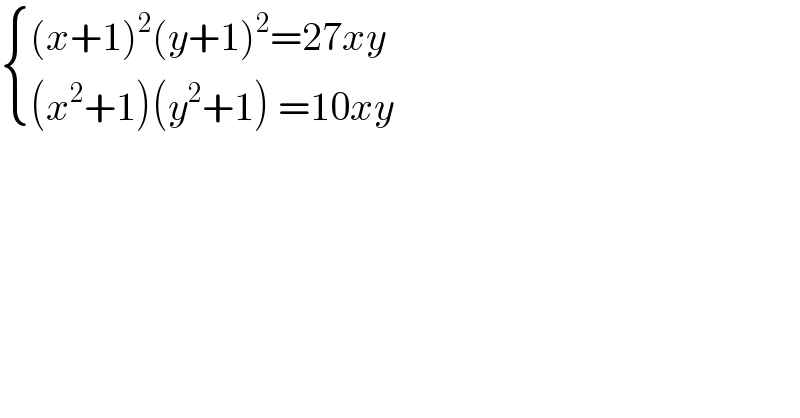
{ (((x+1)^2 (y+1)^2 =27xy)),(((x^2 +1)(y^2 +1) =10xy)) :}
$$\begin{cases}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} \left({y}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{27}{xy}}\\{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({y}^{\mathrm{2}} +\mathrm{1}\right)\:=\mathrm{10}{xy}}\end{cases} \\ $$
Answered by john santu last updated on 13/Apr/20
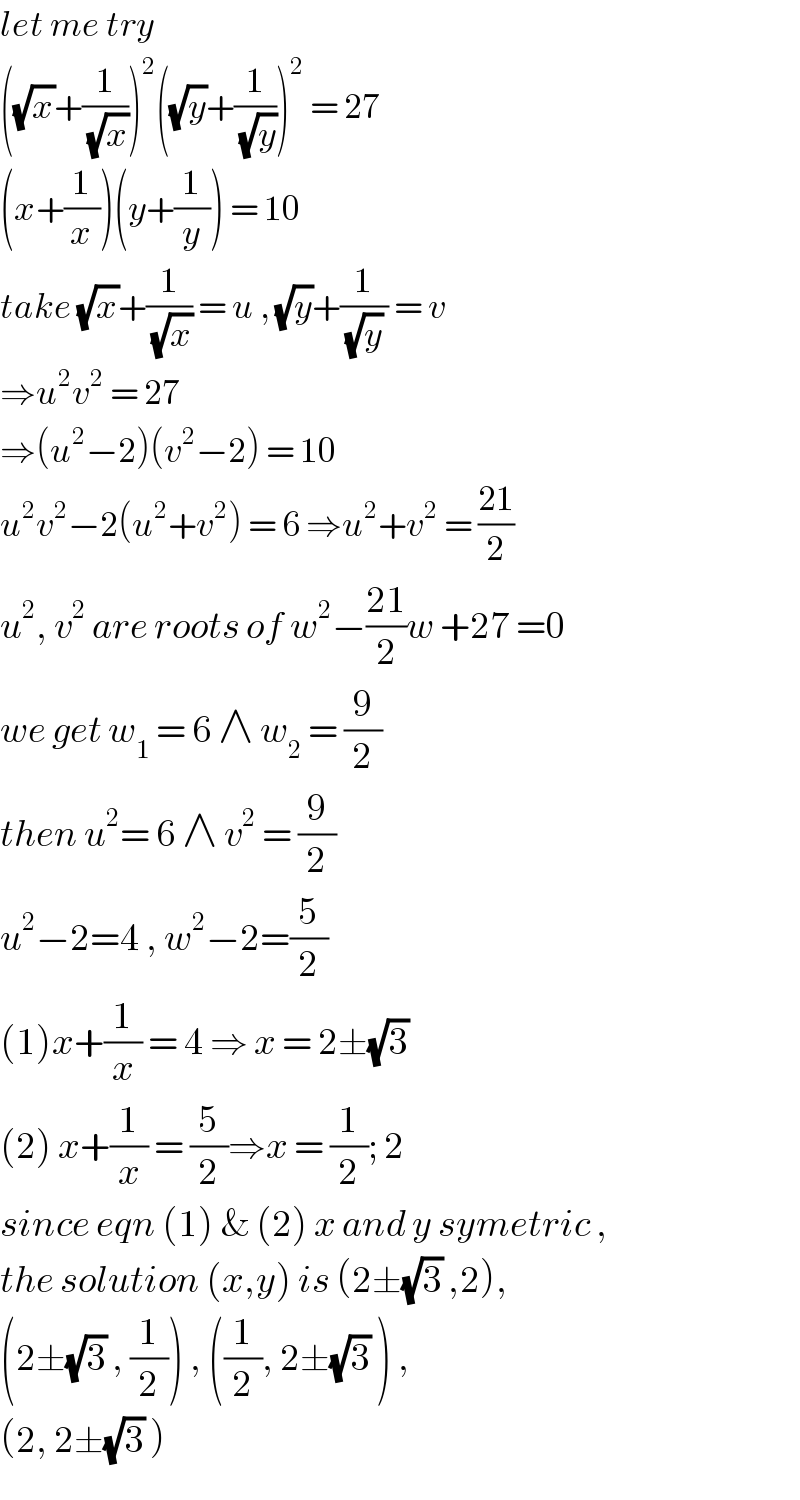
let me try ((√x)+(1/( (√x))))^2 ((√y)+(1/( (√y))))^2 = 27 (x+(1/x))(y+(1/y)) = 10 take (√x)+(1/( (√x))) = u , (√y)+(1/( (√y) )) = v ⇒u^2 v^2 = 27 ⇒(u^2 −2)(v^2 −2) = 10 u^2 v^2 −2(u^2 +v^2 ) = 6 ⇒u^2 +v^2 = ((21)/2) u^2 , v^2 are roots of w^2 −((21)/2)w +27 =0 we get w_1 = 6 ∧ w_2 = (9/2) then u^2 = 6 ∧ v^2 = (9/2) u^2 −2=4 , w^2 −2=(5/2) (1)x+(1/x) = 4 ⇒ x = 2±(√3) (2) x+(1/x) = (5/2)⇒x = (1/2); 2 since eqn (1) & (2) x and y symetric , the solution (x,y) is (2±(√3) ,2), (2±(√3) , (1/2)) , ((1/2), 2±(√3) ) , (2, 2±(√3) )
$${let}\:{me}\:{try}\: \\ $$$$\left(\sqrt{{x}}+\frac{\mathrm{1}}{\:\sqrt{{x}}}\right)^{\mathrm{2}} \left(\sqrt{{y}}+\frac{\mathrm{1}}{\:\sqrt{{y}}}\right)^{\mathrm{2}} \:=\:\mathrm{27} \\ $$$$\left({x}+\frac{\mathrm{1}}{{x}}\right)\left({y}+\frac{\mathrm{1}}{{y}}\right)\:=\:\mathrm{10} \\ $$$${take}\:\sqrt{{x}}+\frac{\mathrm{1}}{\:\sqrt{{x}}}\:=\:{u}\:,\:\sqrt{{y}}+\frac{\mathrm{1}}{\:\sqrt{{y}}\:}\:=\:{v} \\ $$$$\Rightarrow{u}^{\mathrm{2}} {v}^{\mathrm{2}} \:=\:\mathrm{27} \\ $$$$\Rightarrow\left({u}^{\mathrm{2}} −\mathrm{2}\right)\left({v}^{\mathrm{2}} −\mathrm{2}\right)\:=\:\mathrm{10} \\ $$$${u}^{\mathrm{2}} {v}^{\mathrm{2}} −\mathrm{2}\left({u}^{\mathrm{2}} +{v}^{\mathrm{2}} \right)\:=\:\mathrm{6}\:\Rightarrow{u}^{\mathrm{2}} +{v}^{\mathrm{2}} \:=\:\frac{\mathrm{21}}{\mathrm{2}} \\ $$$${u}^{\mathrm{2}} ,\:{v}^{\mathrm{2}} \:{are}\:{roots}\:{of}\:{w}^{\mathrm{2}} −\frac{\mathrm{21}}{\mathrm{2}}{w}\:+\mathrm{27}\:=\mathrm{0} \\ $$$${we}\:{get}\:{w}_{\mathrm{1}} \:=\:\mathrm{6}\:\wedge\:{w}_{\mathrm{2}} \:=\:\frac{\mathrm{9}}{\mathrm{2}} \\ $$$${then}\:{u}^{\mathrm{2}} =\:\mathrm{6}\:\wedge\:{v}^{\mathrm{2}} \:=\:\frac{\mathrm{9}}{\mathrm{2}} \\ $$$${u}^{\mathrm{2}} −\mathrm{2}=\mathrm{4}\:,\:{w}^{\mathrm{2}} −\mathrm{2}=\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$\left(\mathrm{1}\right){x}+\frac{\mathrm{1}}{{x}}\:=\:\mathrm{4}\:\Rightarrow\:{x}\:=\:\mathrm{2}\pm\sqrt{\mathrm{3}} \\ $$$$\left(\mathrm{2}\right)\:{x}+\frac{\mathrm{1}}{{x}}\:=\:\frac{\mathrm{5}}{\mathrm{2}}\Rightarrow{x}\:=\:\frac{\mathrm{1}}{\mathrm{2}};\:\mathrm{2} \\ $$$${since}\:{eqn}\:\left(\mathrm{1}\right)\:\&\:\left(\mathrm{2}\right)\:{x}\:{and}\:{y}\:{symetric}\:,\: \\ $$$${the}\:{solution}\:\left({x},{y}\right)\:{is}\:\left(\mathrm{2}\pm\sqrt{\mathrm{3}}\:,\mathrm{2}\right), \\ $$$$\left(\mathrm{2}\pm\sqrt{\mathrm{3}}\:,\:\frac{\mathrm{1}}{\mathrm{2}}\right)\:,\:\left(\frac{\mathrm{1}}{\mathrm{2}},\:\mathrm{2}\pm\sqrt{\mathrm{3}}\:\right)\:,\: \\ $$$$\left(\mathrm{2},\:\mathrm{2}\pm\sqrt{\mathrm{3}}\:\right) \\ $$
Commented by jagoll last updated on 13/Apr/20
waw...cooll
$${waw}…{cooll} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *