Menu Close

x-1-2x-2-x-1-dx-

Tinku Tara 0 Comments
Pin




Question Number 146110 by puissant last updated on 11/Jul/21
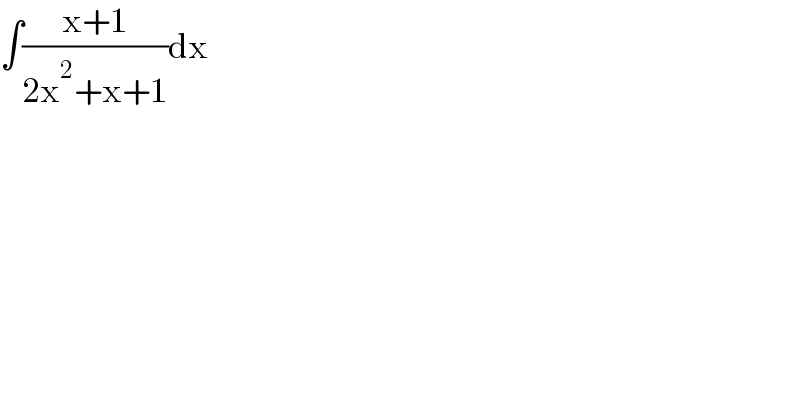
∫((x+1)/(2x^2 +x+1))dx
$$\int\frac{\mathrm{x}+\mathrm{1}}{\mathrm{2x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}\mathrm{dx} \\ $$
Answered by gsk2684 last updated on 11/Jul/21
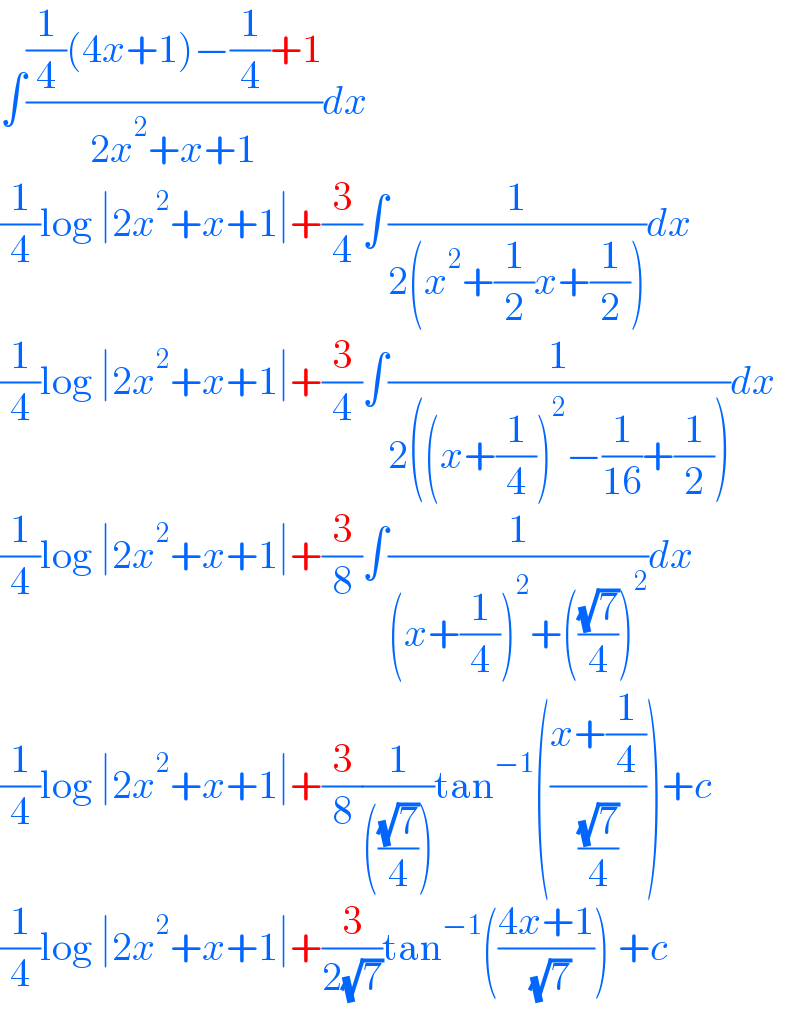
∫(((1/4)(4x+1)−(1/4)+1)/(2x^2 +x+1))dx (1/4)log ∣2x^2 +x+1∣+(3/4)∫(1/(2(x^2 +(1/2)x+(1/2))))dx (1/4)log ∣2x^2 +x+1∣+(3/4)∫(1/(2((x+(1/4))^2 −(1/(16))+(1/2))))dx (1/4)log ∣2x^2 +x+1∣+(3/8)∫(1/((x+(1/4))^2 +(((√7)/4))^2 ))dx (1/4)log ∣2x^2 +x+1∣+(3/8)(1/((((√7)/4))))tan^(−1) (((x+(1/4))/((√7)/4)))+c (1/4)log ∣2x^2 +x+1∣+(3/(2(√7)))tan^(−1) (((4x+1)/( (√7)))) +c
$$\int\frac{\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{4}{x}+\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{4}}+\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} +{x}+\mathrm{1}}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\mathrm{log}\:\mid\mathrm{2}{x}^{\mathrm{2}} +{x}+\mathrm{1}\mid+\frac{\mathrm{3}}{\mathrm{4}}\int\frac{\mathrm{1}}{\mathrm{2}\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\mathrm{log}\:\mid\mathrm{2}{x}^{\mathrm{2}} +{x}+\mathrm{1}\mid+\frac{\mathrm{3}}{\mathrm{4}}\int\frac{\mathrm{1}}{\mathrm{2}\left(\left({x}+\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{16}}+\frac{\mathrm{1}}{\mathrm{2}}\right)}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\mathrm{log}\:\mid\mathrm{2}{x}^{\mathrm{2}} +{x}+\mathrm{1}\mid+\frac{\mathrm{3}}{\mathrm{8}}\int\frac{\mathrm{1}}{\left({x}+\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{7}}}{\mathrm{4}}\right)^{\mathrm{2}} }{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\mathrm{log}\:\mid\mathrm{2}{x}^{\mathrm{2}} +{x}+\mathrm{1}\mid+\frac{\mathrm{3}}{\mathrm{8}}\frac{\mathrm{1}}{\left(\frac{\sqrt{\mathrm{7}}}{\mathrm{4}}\right)}\mathrm{tan}^{−\mathrm{1}} \left(\frac{{x}+\frac{\mathrm{1}}{\mathrm{4}}}{\frac{\sqrt{\mathrm{7}}}{\mathrm{4}}}\right)+{c} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\mathrm{log}\:\mid\mathrm{2}{x}^{\mathrm{2}} +{x}+\mathrm{1}\mid+\frac{\mathrm{3}}{\mathrm{2}\sqrt{\mathrm{7}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{4}{x}+\mathrm{1}}{\:\sqrt{\mathrm{7}}}\right)\:+{c} \\ $$
Commented by puissant last updated on 11/Jul/21
Sir there is an error in the first line.
$$\mathrm{Sir}\:\mathrm{there}\:\mathrm{is}\:\mathrm{an}\:\mathrm{error}\:\mathrm{in}\:\mathrm{the}\:\mathrm{first}\:\mathrm{line}. \\ $$
Commented by gsk2684 last updated on 11/Jul/21
corrected
$${corrected} \\ $$
Commented by puissant last updated on 11/Jul/21
Sir that there is + instead of −
$$\mathrm{Sir}\:\mathrm{that}\:\mathrm{there}\:\mathrm{is}\:+\:\mathrm{instead}\:\mathrm{of}\:−\: \\ $$
Commented by gsk2684 last updated on 11/Jul/21
silly mistakes but mistake
$${silly}\:{mistakes}\:{but}\:{mistake} \\ $$
Commented by puissant last updated on 11/Jul/21
okey sir
$$\mathrm{okey}\:\mathrm{sir} \\ $$
Answered by mathmax by abdo last updated on 11/Jul/21
I=∫ ((x+1)/(2x^2 +x+1))dx ⇒I=(1/4)∫ ((4x+1+3)/(2x^(2 ) +x+1))dx =(1/4)log(2x^2 +x+1)+(3/8)∫ (dx/(x^(2 ) +(x/2)+(1/2))) we have ∫ (dx/(x^2 +(x/2)+(1/2)))=∫ (dx/(x^2 +2(1/4)x +(1/(16))+(1/2)−(1/(16))))=∫ (dx/((x+(1/4))^2 +(7/(16)))) =_(x+(1/4)=((√7)/4)t) ((16)/7) ∫ (1/(t^2 +1))((√7)/4)dt =(4/( (√7))) arctan(t)+k =(4/( (√7)))arctan(((4x+1)/( (√7))))+K ⇒ I=(1/4)log(2x^2 +x+1)+(3/(2(√7))) arctan(((4x+1)/( (√7))))+K
$$\mathrm{I}=\int\:\frac{\mathrm{x}+\mathrm{1}}{\mathrm{2x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}\mathrm{dx}\:\Rightarrow\mathrm{I}=\frac{\mathrm{1}}{\mathrm{4}}\int\:\frac{\mathrm{4x}+\mathrm{1}+\mathrm{3}}{\mathrm{2x}^{\mathrm{2}\:} +\mathrm{x}+\mathrm{1}}\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{log}\left(\mathrm{2x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{1}\right)+\frac{\mathrm{3}}{\mathrm{8}}\int\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}\:} +\frac{\mathrm{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}}\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\int\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \:+\frac{\mathrm{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}}=\int\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{2}\frac{\mathrm{1}}{\mathrm{4}}\mathrm{x}\:+\frac{\mathrm{1}}{\mathrm{16}}+\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{16}}}=\int\:\:\frac{\mathrm{dx}}{\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{2}} +\frac{\mathrm{7}}{\mathrm{16}}} \\ $$$$=_{\mathrm{x}+\frac{\mathrm{1}}{\mathrm{4}}=\frac{\sqrt{\mathrm{7}}}{\mathrm{4}}\mathrm{t}} \:\:\frac{\mathrm{16}}{\mathrm{7}}\:\int\:\:\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\frac{\sqrt{\mathrm{7}}}{\mathrm{4}}\mathrm{dt}\:=\frac{\mathrm{4}}{\:\sqrt{\mathrm{7}}}\:\mathrm{arctan}\left(\mathrm{t}\right)+\mathrm{k} \\ $$$$=\frac{\mathrm{4}}{\:\sqrt{\mathrm{7}}}\mathrm{arctan}\left(\frac{\mathrm{4x}+\mathrm{1}}{\:\sqrt{\mathrm{7}}}\right)+\mathrm{K}\:\Rightarrow \\ $$$$\mathrm{I}=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{log}\left(\mathrm{2x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{1}\right)+\frac{\mathrm{3}}{\mathrm{2}\sqrt{\mathrm{7}}}\:\mathrm{arctan}\left(\frac{\mathrm{4x}+\mathrm{1}}{\:\sqrt{\mathrm{7}}}\right)+\mathrm{K} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *