x-1-3-2-log-x-11-11-x-

Question Number 181579 by mathlove last updated on 27/Nov/22

{(\sqrt[3]{x})}^{- 2 + {l o g}_{x} 11} = 11

x = ?

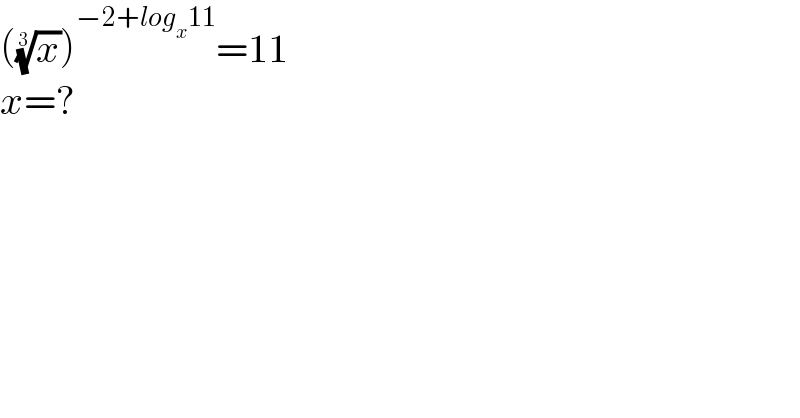
Commented by Socracious last updated on 27/Nov/22

x = \frac{1}{11}

Answered by Frix last updated on 27/Nov/22

x > 0

x^{- \frac{2}{3} + \frac{\ln 11}{3 \ln x}} = 11

x^{- \frac{2}{3}} x^{\frac{\ln 11}{3 \ln x}} = 11

x^{- \frac{2}{3}} 11^{\frac{1}{3}} = 11

x^{- \frac{2}{3}} = 11^{\frac{2}{3}}

x = \frac{1}{11}

Commented by mathlove last updated on 27/Nov/22

w a y x^{\frac{l n 11}{3 l n x}} \overset{?}{=} 11^{\frac{1}{3}} ?

Commented by mathlove last updated on 27/Nov/22

t h a n k s