Question Number 85358 by jagoll last updated on 21/Mar/20

Answered by john santu last updated on 21/Mar/20
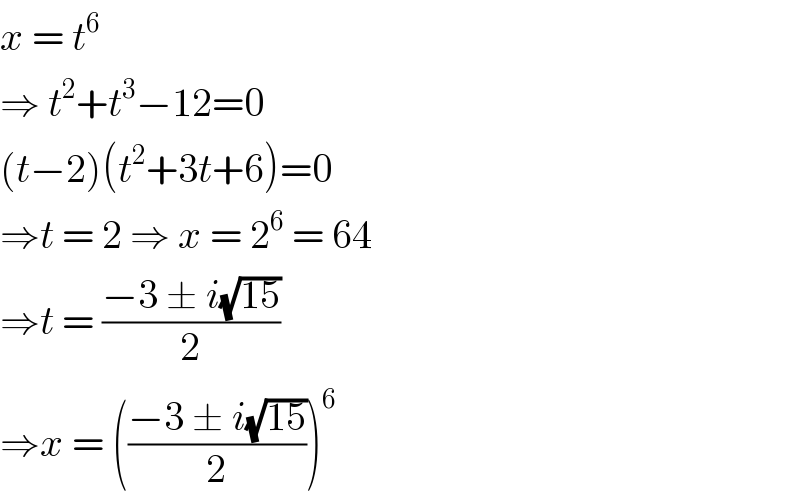
Commented by john santu last updated on 21/Mar/20
Commented by MJS last updated on 21/Mar/20
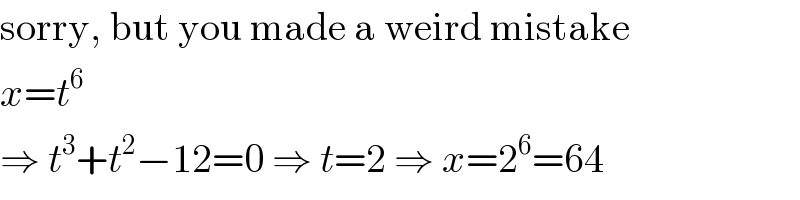
Commented by MJS last updated on 21/Mar/20