Question Number 58045 by ANTARES VY last updated on 17/Apr/19
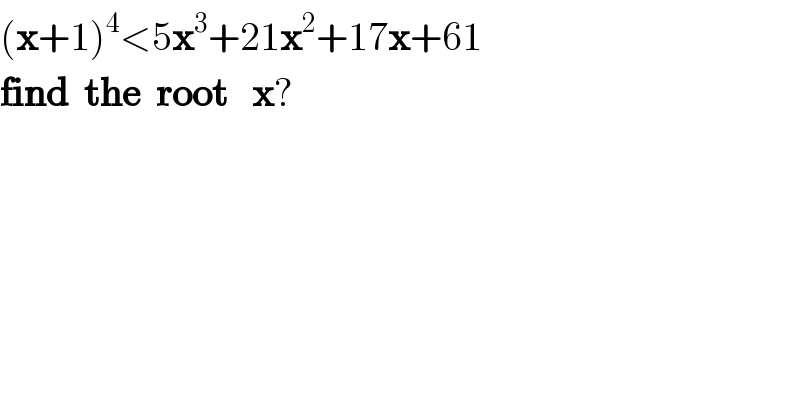
$$\left(\boldsymbol{\mathrm{x}}+\mathrm{1}\right)^{\mathrm{4}} <\mathrm{5}\boldsymbol{\mathrm{x}}^{\mathrm{3}} +\mathrm{21}\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{17}\boldsymbol{\mathrm{x}}+\mathrm{61} \\ $$$$\boldsymbol{\mathrm{find}}\:\:\boldsymbol{\mathrm{the}}\:\:\boldsymbol{\mathrm{root}}\:\:\:\boldsymbol{\mathrm{x}}? \\ $$
Answered by tanmay last updated on 17/Apr/19
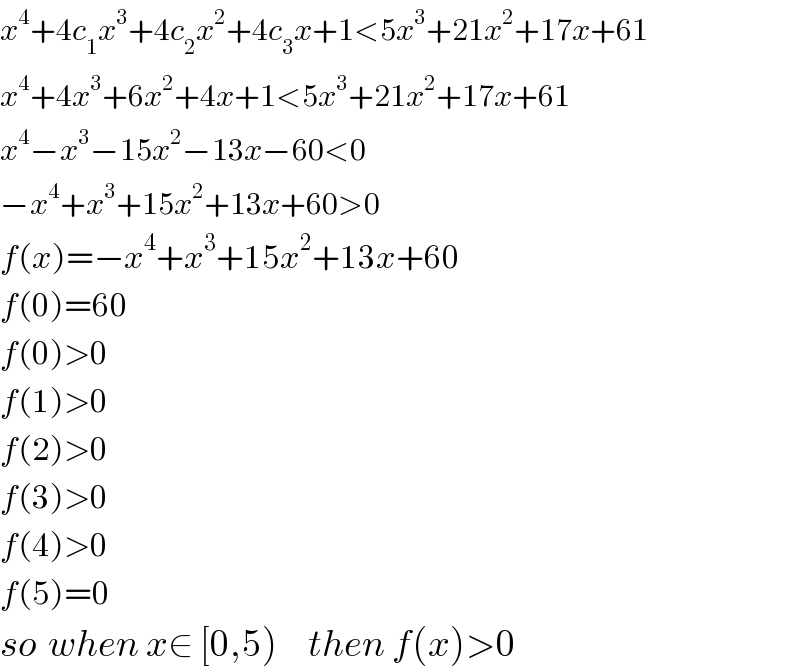
$${x}^{\mathrm{4}} +\mathrm{4}{c}_{\mathrm{1}} {x}^{\mathrm{3}} +\mathrm{4}{c}_{\mathrm{2}} {x}^{\mathrm{2}} +\mathrm{4}{c}_{\mathrm{3}} {x}+\mathrm{1}<\mathrm{5}{x}^{\mathrm{3}} +\mathrm{21}{x}^{\mathrm{2}} +\mathrm{17}{x}+\mathrm{61} \\ $$$${x}^{\mathrm{4}} +\mathrm{4}{x}^{\mathrm{3}} +\mathrm{6}{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{1}<\mathrm{5}{x}^{\mathrm{3}} +\mathrm{21}{x}^{\mathrm{2}} +\mathrm{17}{x}+\mathrm{61} \\ $$$${x}^{\mathrm{4}} −{x}^{\mathrm{3}} −\mathrm{15}{x}^{\mathrm{2}} −\mathrm{13}{x}−\mathrm{60}<\mathrm{0} \\ $$$$−{x}^{\mathrm{4}} +{x}^{\mathrm{3}} +\mathrm{15}{x}^{\mathrm{2}} +\mathrm{13}{x}+\mathrm{60}>\mathrm{0} \\ $$$${f}\left({x}\right)=−{x}^{\mathrm{4}} +{x}^{\mathrm{3}} +\mathrm{15}{x}^{\mathrm{2}} +\mathrm{13}{x}+\mathrm{60} \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{60}\: \\ $$$${f}\left(\mathrm{0}\right)>\mathrm{0} \\ $$$${f}\left(\mathrm{1}\right)>\mathrm{0} \\ $$$${f}\left(\mathrm{2}\right)>\mathrm{0} \\ $$$${f}\left(\mathrm{3}\right)>\mathrm{0} \\ $$$${f}\left(\mathrm{4}\right)>\mathrm{0} \\ $$$${f}\left(\mathrm{5}\right)=\mathrm{0} \\ $$$${so}\:\:{when}\:{x}\in\:\left[\mathrm{0},\mathrm{5}\right)\:\:\:\:\:{then}\:{f}\left({x}\right)>\mathrm{0} \\ $$
