Question Number 162715 by tounghoungko last updated on 31/Dec/21
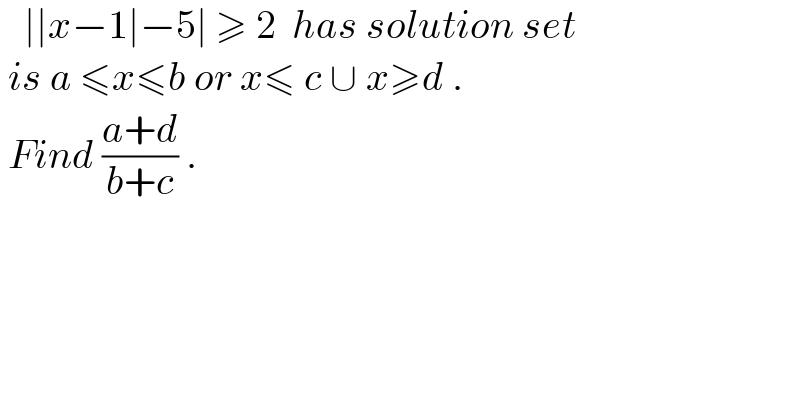
$$\:\:\:\mid\mid{x}−\mathrm{1}\mid−\mathrm{5}\mid\:\geqslant\:\mathrm{2}\:\:{has}\:{solution}\:{set} \\ $$$$\:{is}\:{a}\:\leqslant{x}\leqslant{b}\:{or}\:{x}\leqslant\:{c}\:\cup\:{x}\geqslant{d}\:. \\ $$$$\:{Find}\:\frac{{a}+{d}}{{b}+{c}}\:. \\ $$
Answered by bobhans last updated on 01/Jan/22

$$\:\mid\mid\mathrm{x}−\mathrm{1}\mid−\mathrm{5}\mid\:\geqslant\mathrm{2}\:\Rightarrow\:\left(\mid\mathrm{x}−\mathrm{1}\mid−\mathrm{7}\right)\left(\mid\mathrm{x}−\mathrm{1}\mid−\mathrm{3}\right)\geqslant\mathrm{0} \\ $$$$\:\Rightarrow\:\mid\mathrm{x}−\mathrm{1}\mid\:\leqslant\mathrm{3}\:\cup\:\mid\mathrm{x}−\mathrm{1}\mid\:\geqslant\mathrm{7} \\ $$$$\:\Rightarrow\:−\mathrm{2}\leqslant\mathrm{x}\leqslant\mathrm{4}\:\cup\:\mathrm{x}\leqslant−\mathrm{6}\:\cup\:\mathrm{x}\geqslant\:\mathrm{8} \\ $$$$\:\begin{cases}{\mathrm{a}=−\mathrm{2}\:\wedge\:\mathrm{b}=\mathrm{4}\:}\\{\mathrm{c}=−\mathrm{6}\:\wedge\:\mathrm{d}=\mathrm{8}}\end{cases}\:\Rightarrow\frac{\mathrm{a}+\mathrm{d}}{\mathrm{b}+\mathrm{c}}\:=\:\frac{\mathrm{6}}{−\mathrm{2}}=\:−\mathrm{3} \\ $$
Answered by MJS_new last updated on 31/Dec/21
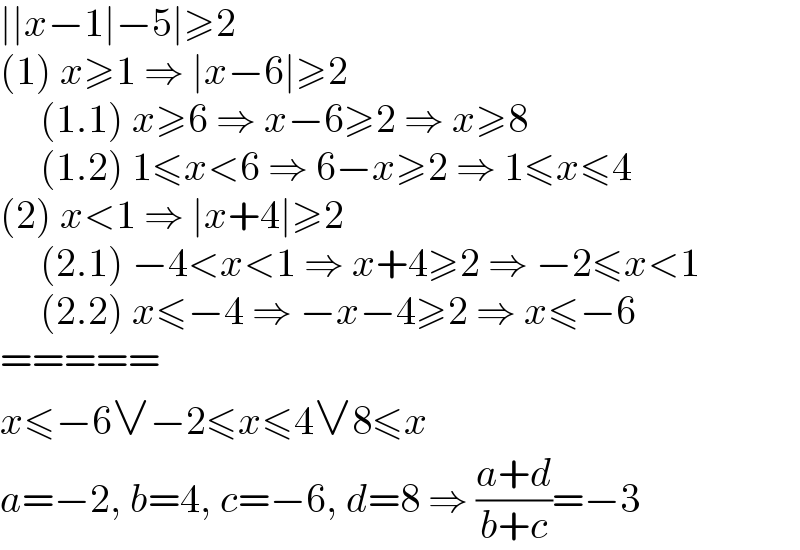
$$\mid\mid{x}−\mathrm{1}\mid−\mathrm{5}\mid\geqslant\mathrm{2} \\ $$$$\left(\mathrm{1}\right)\:{x}\geqslant\mathrm{1}\:\Rightarrow\:\mid{x}−\mathrm{6}\mid\geqslant\mathrm{2} \\ $$$$\:\:\:\:\:\left(\mathrm{1}.\mathrm{1}\right)\:{x}\geqslant\mathrm{6}\:\Rightarrow\:{x}−\mathrm{6}\geqslant\mathrm{2}\:\Rightarrow\:{x}\geqslant\mathrm{8} \\ $$$$\:\:\:\:\:\left(\mathrm{1}.\mathrm{2}\right)\:\mathrm{1}\leqslant{x}<\mathrm{6}\:\Rightarrow\:\mathrm{6}−{x}\geqslant\mathrm{2}\:\Rightarrow\:\mathrm{1}\leqslant{x}\leqslant\mathrm{4} \\ $$$$\left(\mathrm{2}\right)\:{x}<\mathrm{1}\:\Rightarrow\:\mid{x}+\mathrm{4}\mid\geqslant\mathrm{2} \\ $$$$\:\:\:\:\:\left(\mathrm{2}.\mathrm{1}\right)\:−\mathrm{4}<{x}<\mathrm{1}\:\Rightarrow\:{x}+\mathrm{4}\geqslant\mathrm{2}\:\Rightarrow\:−\mathrm{2}\leqslant{x}<\mathrm{1} \\ $$$$\:\:\:\:\:\left(\mathrm{2}.\mathrm{2}\right)\:{x}\leqslant−\mathrm{4}\:\Rightarrow\:−{x}−\mathrm{4}\geqslant\mathrm{2}\:\Rightarrow\:{x}\leqslant−\mathrm{6} \\ $$$$===== \\ $$$${x}\leqslant−\mathrm{6}\vee−\mathrm{2}\leqslant{x}\leqslant\mathrm{4}\vee\mathrm{8}\leqslant{x} \\ $$$${a}=−\mathrm{2},\:{b}=\mathrm{4},\:{c}=−\mathrm{6},\:{d}=\mathrm{8}\:\Rightarrow\:\frac{{a}+{d}}{{b}+{c}}=−\mathrm{3} \\ $$
