Menu Close

x-1-csc-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 174628 by cortano1 last updated on 06/Aug/22
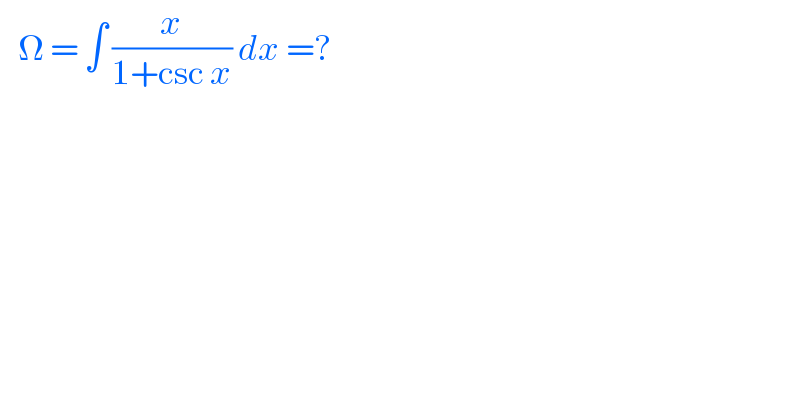
Ω = ∫ (x/(1+csc x)) dx =?
$$\:\:\:\Omega\:=\:\int\:\frac{{x}}{\mathrm{1}+\mathrm{csc}\:{x}}\:{dx}\:=? \\ $$
Commented by infinityaction last updated on 06/Aug/22
∫(x/(1+cscx))dx=∫((xsinx)/(1+sinx))dx =∫x((1+sinx−1)/(1+sinx))dx=∫(x−(x/(1+sinx)))dx Ω = (x^2 /2)−∫(x/(1+sinx_(I) )) I = ∫(x/(1+sinx )) ⇒ I = ∫(x/(1+cos((π/2) −x))) I =∫(x/(2cos^2 ((π/4) −(x/2)))) (π/4)−(x/2) = y ⇒ (dx/2) = −dy I = −∫((((π/2)−2y)dy)/(cos^2 y )) I = 2∫ysec^2 y dy −(π/2)∫sec^2 y dy I = 2ytany −log ∣siny∣ −(π/2)tany +C Ω = (x^2 /2)+log∣siny∣ +(π/2)tany −2ytany+C here y = (π/4)−(x/2)
$$\int\frac{{x}}{\mathrm{1}+\mathrm{csc}{x}}{dx}=\int\frac{{xs}\mathrm{in}{x}}{\mathrm{1}+\mathrm{sin}{x}}{dx} \\ $$$$=\int{x}\frac{\mathrm{1}+\mathrm{sin}{x}−\mathrm{1}}{\mathrm{1}+\mathrm{sin}{x}}{dx}=\int\left({x}−\frac{{x}}{\mathrm{1}+\mathrm{sin}{x}}\right){dx} \\ $$$$\Omega\:=\:\frac{{x}^{\mathrm{2}} }{\mathrm{2}}−\int\frac{{x}}{\underset{{I}} {\underbrace{\mathrm{1}+\mathrm{sin}{x}}}\:} \\ $$$$\:{I}\:=\:\int\frac{{x}}{\mathrm{1}+\mathrm{sin}{x}\:}\:\:\:\Rightarrow\:{I}\:\:=\:\:\int\frac{{x}}{\mathrm{1}+\mathrm{cos}\left(\frac{\pi}{\mathrm{2}}\:−{x}\right)} \\ $$$${I}\:\:=\int\frac{{x}}{\mathrm{2cos}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{4}}\:−\frac{{x}}{\mathrm{2}}\right)} \\ $$$$\frac{\pi}{\mathrm{4}}−\frac{{x}}{\mathrm{2}}\:\:=\:{y}\:\Rightarrow\:\frac{{dx}}{\mathrm{2}}\:\:=\:−{dy} \\ $$$${I}\:=\:−\int\frac{\left(\frac{\pi}{\mathrm{2}}−\mathrm{2}{y}\right){dy}}{\mathrm{cos}^{\mathrm{2}} {y}\:} \\ $$$${I}\:\:=\:\:\mathrm{2}\int{y}\mathrm{sec}^{\mathrm{2}} {y}\:{dy}\:−\frac{\pi}{\mathrm{2}}\int\mathrm{sec}^{\mathrm{2}} {y}\:{dy} \\ $$$${I}\:=\:\mathrm{2}{y}\mathrm{tan}{y}\:−\mathrm{log}\:\mid\mathrm{sin}{y}\mid\:−\frac{\pi}{\mathrm{2}}\mathrm{tan}{y}\:+{C} \\ $$$$\Omega\:=\:\:\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{log}\mid\mathrm{sin}{y}\mid\:+\frac{\pi}{\mathrm{2}}\mathrm{tan}{y}\:−\mathrm{2}{y}\mathrm{tan}{y}+{C} \\ $$$$\:\:\:{here}\:\:\:{y}\:\:=\:\:\frac{\pi}{\mathrm{4}}−\frac{{x}}{\mathrm{2}}\:\:\:\: \\ $$
Commented by Tawa11 last updated on 09/Aug/22
Great sir
$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by aleks041103 last updated on 06/Aug/22
∫(x/(1+cscx))dx=∫((xsinx)/(1+sinx))dx= =∫x((1+sinx−1)/(1+sinx))dx=∫(x−(x/(1+sinx)))dx= =(x^2 /2)−∫((xdx)/(1+sinx))=(x^2 /2)+I z=tan(x/2)⇒x=2arctan(z)⇒dx=((2dz)/(1+z^2 )) sin(x)=2sin(x/2)cos(x/2)= =2tan(x/2)cos^2 (x/2)= =((2tan(x/2))/(1+tan^2 (x/2)))=((2z)/(1+z^2 )) ⇒(1/(1+sinx))=((1+z^2 )/((1+z)^2 )) ⇒I=4∫arctan(z)(−(dz/((1+z)^2 )))= =4∫arctan(z)d((1/(1+z)))= =((4arctan(z))/(1+z))−4∫(dz/((1+z)(1+z^2 )))= =((2x)/(1+tan(x/2)))+2∫((−2dz)/((1+z)(1+z^2 ))) ((−2)/((1+z)(1+z^2 )))=(a/(1+z))+((bz+c)/(1+z^2 )) ⇒a+az^2 +bz+c+bz^2 +cz=−2 a+c=−2, b+c=0, a+b=0⇒−a=−c=b=1 ⇒∫((−2dz)/((1+z)(1+z^2 )))=∫(((z−1)/(1+z^2 ))−(1/(1+z)))dz= =∫((zdz)/(1+z^2 ))−∫(dz/(1+z^2 ))−∫(dz/(1+z))= =(1/2)∫((d(1+z^2 ))/(1+z^2 ))−arctan(z)−ln(1+z)= =(1/2)ln(1+z^2 )−ln(1+z)−arctan(z)+C= =(1/2)ln(((1+z^2 )/((1+z)^2 )))−arctan(z)+C= =−(1/2)ln(1+sinx)−(1/2)x+C ⇒I=((2x)/(1+tan(x/2)))−x−ln(1+sinx)+C ⇒∫(x/(1+cscx))dx=(x^2 /2)+((2x)/(1+tan(x/2)))−x−ln(1+sinx)+C
$$\int\frac{{x}}{\mathrm{1}+{cscx}}{dx}=\int\frac{{xsinx}}{\mathrm{1}+{sinx}}{dx}= \\ $$$$=\int{x}\frac{\mathrm{1}+{sinx}−\mathrm{1}}{\mathrm{1}+{sinx}}{dx}=\int\left({x}−\frac{{x}}{\mathrm{1}+{sinx}}\right){dx}= \\ $$$$=\frac{{x}^{\mathrm{2}} }{\mathrm{2}}−\int\frac{{xdx}}{\mathrm{1}+{sinx}}=\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+{I} \\ $$$${z}={tan}\left({x}/\mathrm{2}\right)\Rightarrow{x}=\mathrm{2}{arctan}\left({z}\right)\Rightarrow{dx}=\frac{\mathrm{2}{dz}}{\mathrm{1}+{z}^{\mathrm{2}} } \\ $$$${sin}\left({x}\right)=\mathrm{2}{sin}\left({x}/\mathrm{2}\right){cos}\left({x}/\mathrm{2}\right)= \\ $$$$=\mathrm{2}{tan}\left({x}/\mathrm{2}\right){cos}^{\mathrm{2}} \left({x}/\mathrm{2}\right)= \\ $$$$=\frac{\mathrm{2}{tan}\left({x}/\mathrm{2}\right)}{\mathrm{1}+{tan}^{\mathrm{2}} \left({x}/\mathrm{2}\right)}=\frac{\mathrm{2}{z}}{\mathrm{1}+{z}^{\mathrm{2}} } \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{1}+{sinx}}=\frac{\mathrm{1}+{z}^{\mathrm{2}} }{\left(\mathrm{1}+{z}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow{I}=\mathrm{4}\int{arctan}\left({z}\right)\left(−\frac{{dz}}{\left(\mathrm{1}+{z}\right)^{\mathrm{2}} }\right)= \\ $$$$=\mathrm{4}\int{arctan}\left({z}\right){d}\left(\frac{\mathrm{1}}{\mathrm{1}+{z}}\right)= \\ $$$$=\frac{\mathrm{4}{arctan}\left({z}\right)}{\mathrm{1}+{z}}−\mathrm{4}\int\frac{{dz}}{\left(\mathrm{1}+{z}\right)\left(\mathrm{1}+{z}^{\mathrm{2}} \right)}= \\ $$$$=\frac{\mathrm{2}{x}}{\mathrm{1}+{tan}\left({x}/\mathrm{2}\right)}+\mathrm{2}\int\frac{−\mathrm{2}{dz}}{\left(\mathrm{1}+{z}\right)\left(\mathrm{1}+{z}^{\mathrm{2}} \right)} \\ $$$$\frac{−\mathrm{2}}{\left(\mathrm{1}+{z}\right)\left(\mathrm{1}+{z}^{\mathrm{2}} \right)}=\frac{{a}}{\mathrm{1}+{z}}+\frac{{bz}+{c}}{\mathrm{1}+{z}^{\mathrm{2}} } \\ $$$$\Rightarrow{a}+{az}^{\mathrm{2}} +{bz}+{c}+{bz}^{\mathrm{2}} +{cz}=−\mathrm{2} \\ $$$${a}+{c}=−\mathrm{2},\:{b}+{c}=\mathrm{0},\:{a}+{b}=\mathrm{0}\Rightarrow−{a}=−{c}={b}=\mathrm{1} \\ $$$$\Rightarrow\int\frac{−\mathrm{2}{dz}}{\left(\mathrm{1}+{z}\right)\left(\mathrm{1}+{z}^{\mathrm{2}} \right)}=\int\left(\frac{{z}−\mathrm{1}}{\mathrm{1}+{z}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{1}+{z}}\right){dz}= \\ $$$$=\int\frac{{zdz}}{\mathrm{1}+{z}^{\mathrm{2}} }−\int\frac{{dz}}{\mathrm{1}+{z}^{\mathrm{2}} }−\int\frac{{dz}}{\mathrm{1}+{z}}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left(\mathrm{1}+{z}^{\mathrm{2}} \right)}{\mathrm{1}+{z}^{\mathrm{2}} }−{arctan}\left({z}\right)−{ln}\left(\mathrm{1}+{z}\right)= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+{z}^{\mathrm{2}} \right)−{ln}\left(\mathrm{1}+{z}\right)−{arctan}\left({z}\right)+{C}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{\mathrm{1}+{z}^{\mathrm{2}} }{\left(\mathrm{1}+{z}\right)^{\mathrm{2}} }\right)−{arctan}\left({z}\right)+{C}= \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+{sinx}\right)−\frac{\mathrm{1}}{\mathrm{2}}{x}+{C} \\ $$$$\Rightarrow{I}=\frac{\mathrm{2}{x}}{\mathrm{1}+{tan}\left({x}/\mathrm{2}\right)}−{x}−{ln}\left(\mathrm{1}+{sinx}\right)+{C} \\ $$$$\Rightarrow\int\frac{{x}}{\mathrm{1}+{cscx}}{dx}=\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{2}{x}}{\mathrm{1}+{tan}\left({x}/\mathrm{2}\right)}−{x}−{ln}\left(\mathrm{1}+{sinx}\right)+{C} \\ $$
Commented by Tawa11 last updated on 09/Aug/22
Great sir
$$\mathrm{Great}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *