Menu Close

x-1-lt-x-2-2x-2-solve-for-x-

Tinku Tara 0 Comments
Pin




Question Number 122322 by EngLewis last updated on 15/Nov/20
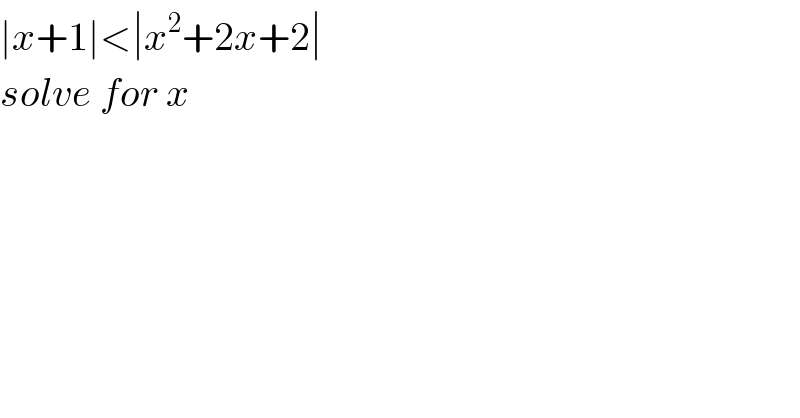
∣x+1∣<∣x^2 +2x+2∣ solve for x
$$\mid{x}+\mathrm{1}\mid<\mid{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}\mid \\ $$$${solve}\:{for}\:{x} \\ $$
Answered by mathmax by abdo last updated on 15/Nov/20
we have x^2 +2x+2 =(x+1)^2 +1>0 ⇒∣x^2 +2x+2∣=x^2 +2x+2 e⇒∣x+1∣−x^2 −2x−2<0 let f(x)=∣x+1∣−x^2 −2x−2 x −∞ −1 +∞ ∣x+1∣ −x−1 0 x+1 f(x) −x^2 −3x−3 −x^2 −x−1 ⇒ f(x)= { ((−x^2 −3x−3 ,x≤−1)),((−x^2 −x−1 ,x≥−1)) :} case1 x≤−1 f(x)<0 ⇒−x^2 −3x−3<0 ⇒x^2 +3x+3>0 Δ=9−12 =−3 ⇒this polynom is slways >0 ⇒S_1 =]−∞ ,−1] case2 x≥1 f(x)<0 ⇒−x^2 −x−1<0 ⇒x^2 +x+1>0 this polynom is also >0 ⇒S_2 =[−1,+∞[ so S =∪ S_i =R
$$\mathrm{we}\:\mathrm{have}\:\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}+\mathrm{2}\:=\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{1}>\mathrm{0}\:\Rightarrow\mid\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}+\mathrm{2}\mid=\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}+\mathrm{2} \\ $$$$\mathrm{e}\Rightarrow\mid\mathrm{x}+\mathrm{1}\mid−\mathrm{x}^{\mathrm{2}} −\mathrm{2x}−\mathrm{2}<\mathrm{0}\:\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)=\mid\mathrm{x}+\mathrm{1}\mid−\mathrm{x}^{\mathrm{2}} −\mathrm{2x}−\mathrm{2} \\ $$$$\mathrm{x}\:\:\:\:\:\:\:\:\:\:\:\:\:−\infty\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\infty \\ $$$$\mid\mathrm{x}+\mathrm{1}\mid\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{x}−\mathrm{1}\:\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\mathrm{x}+\mathrm{1} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{x}^{\mathrm{2}} −\mathrm{3x}−\mathrm{3}\:\:\:\:\:\:\:\:\:\:−\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{1}\: \\ $$$$\Rightarrow\:\mathrm{f}\left(\mathrm{x}\right)=\begin{cases}{−\mathrm{x}^{\mathrm{2}} −\mathrm{3x}−\mathrm{3}\:\:,\mathrm{x}\leqslant−\mathrm{1}}\\{−\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{1}\:,\mathrm{x}\geqslant−\mathrm{1}}\end{cases} \\ $$$$\mathrm{case1}\:\:\mathrm{x}\leqslant−\mathrm{1}\:\:\:\mathrm{f}\left(\mathrm{x}\right)<\mathrm{0}\:\Rightarrow−\mathrm{x}^{\mathrm{2}} −\mathrm{3x}−\mathrm{3}<\mathrm{0}\:\Rightarrow\mathrm{x}^{\mathrm{2}} \:+\mathrm{3x}+\mathrm{3}>\mathrm{0} \\ $$$$\left.\Delta\left.=\mathrm{9}−\mathrm{12}\:=−\mathrm{3}\:\Rightarrow\mathrm{this}\:\mathrm{polynom}\:\mathrm{is}\:\mathrm{slways}\:>\mathrm{0}\:\Rightarrow\mathrm{S}_{\mathrm{1}} =\right]−\infty\:,−\mathrm{1}\right] \\ $$$$\mathrm{case2}\:\:\mathrm{x}\geqslant\mathrm{1}\:\:\mathrm{f}\left(\mathrm{x}\right)<\mathrm{0}\:\Rightarrow−\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{1}<\mathrm{0}\:\Rightarrow\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{1}>\mathrm{0} \\ $$$$\mathrm{this}\:\mathrm{polynom}\:\mathrm{is}\:\mathrm{also}\:>\mathrm{0}\:\Rightarrow\mathrm{S}_{\mathrm{2}} =\left[−\mathrm{1},+\infty\left[\:\:\mathrm{so}\right.\right. \\ $$$$\mathrm{S}\:=\cup\:\mathrm{S}_{\mathrm{i}} =\mathrm{R}\: \\ $$
Answered by MJS_new last updated on 15/Nov/20
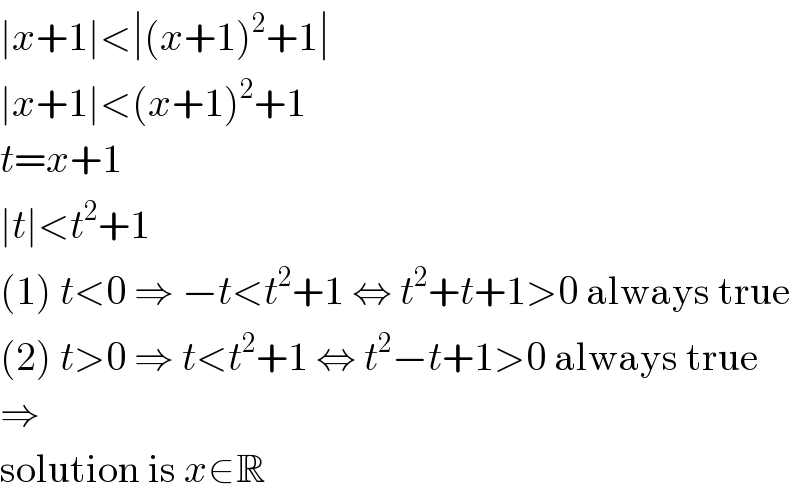
∣x+1∣<∣(x+1)^2 +1∣ ∣x+1∣<(x+1)^2 +1 t=x+1 ∣t∣<t^2 +1 (1) t<0 ⇒ −t<t^2 +1 ⇔ t^2 +t+1>0 always true (2) t>0 ⇒ t<t^2 +1 ⇔ t^2 −t+1>0 always true ⇒ solution is x∈R
$$\mid{x}+\mathrm{1}\mid<\mid\left({x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}\mid \\ $$$$\mid{x}+\mathrm{1}\mid<\left({x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1} \\ $$$${t}={x}+\mathrm{1} \\ $$$$\mid{t}\mid<{t}^{\mathrm{2}} +\mathrm{1} \\ $$$$\left(\mathrm{1}\right)\:{t}<\mathrm{0}\:\Rightarrow\:−{t}<{t}^{\mathrm{2}} +\mathrm{1}\:\Leftrightarrow\:{t}^{\mathrm{2}} +{t}+\mathrm{1}>\mathrm{0}\:\mathrm{always}\:\mathrm{true} \\ $$$$\left(\mathrm{2}\right)\:{t}>\mathrm{0}\:\Rightarrow\:{t}<{t}^{\mathrm{2}} +\mathrm{1}\:\Leftrightarrow\:{t}^{\mathrm{2}} −{t}+\mathrm{1}>\mathrm{0}\:\mathrm{always}\:\mathrm{true} \\ $$$$\Rightarrow \\ $$$$\mathrm{solution}\:\mathrm{is}\:{x}\in\mathbb{R} \\ $$
Answered by mathmax by abdo last updated on 15/Nov/20
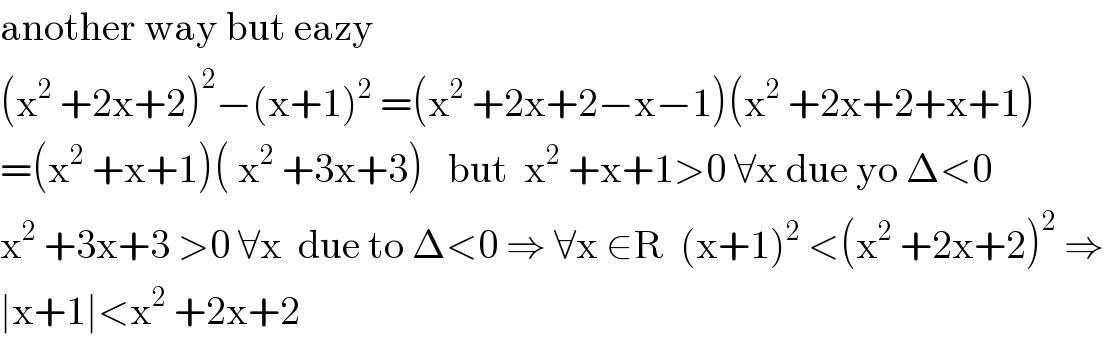
another way but eazy (x^2 +2x+2)^2 −(x+1)^2 =(x^2 +2x+2−x−1)(x^2 +2x+2+x+1) =(x^2 +x+1)( x^2 +3x+3) but x^2 +x+1>0 ∀x due yo Δ<0 x^2 +3x+3 >0 ∀x due to Δ<0 ⇒ ∀x ∈R (x+1)^2 <(x^2 +2x+2)^2 ⇒ ∣x+1∣<x^2 +2x+2
$$\mathrm{another}\:\mathrm{way}\:\mathrm{but}\:\mathrm{eazy} \\ $$$$\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}+\mathrm{2}\right)^{\mathrm{2}} −\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \:=\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}+\mathrm{2}−\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}+\mathrm{2}+\mathrm{x}+\mathrm{1}\right) \\ $$$$=\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{1}\right)\left(\:\mathrm{x}^{\mathrm{2}} \:+\mathrm{3x}+\mathrm{3}\right)\:\:\:\mathrm{but}\:\:\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{1}>\mathrm{0}\:\forall\mathrm{x}\:\mathrm{due}\:\mathrm{yo}\:\Delta<\mathrm{0} \\ $$$$\mathrm{x}^{\mathrm{2}} \:+\mathrm{3x}+\mathrm{3}\:>\mathrm{0}\:\forall\mathrm{x}\:\:\mathrm{due}\:\mathrm{to}\:\Delta<\mathrm{0}\:\Rightarrow\:\forall\mathrm{x}\:\in\mathrm{R}\:\:\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \:<\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}+\mathrm{2}\right)^{\mathrm{2}} \:\Rightarrow \\ $$$$\mid\mathrm{x}+\mathrm{1}\mid<\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}+\mathrm{2} \\ $$
Answered by TANMAY PANACEA last updated on 16/Nov/20
x^2 +2x+2 (x+1)^2 +1 (x+1)^2 always positive so (x+1)^2 +1 always greater than (x+1)
$${x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2} \\ $$$$\left({x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1} \\ $$$$\left({x}+\mathrm{1}\right)^{\mathrm{2}} \:{always}\:{positive} \\ $$$${so}\:\left({x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}\:{always}\:{greater}\:{than}\:\left({x}+\mathrm{1}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *