x-1-sin-x-dx-

Question Number 101192 by bemath last updated on 01/Jul/20

$$\int\:\frac{{x}}{\mathrm{1}+\mathrm{sin}\:{x}}\:{dx}\: \\ $$

Commented by bobhans last updated on 01/Jul/20

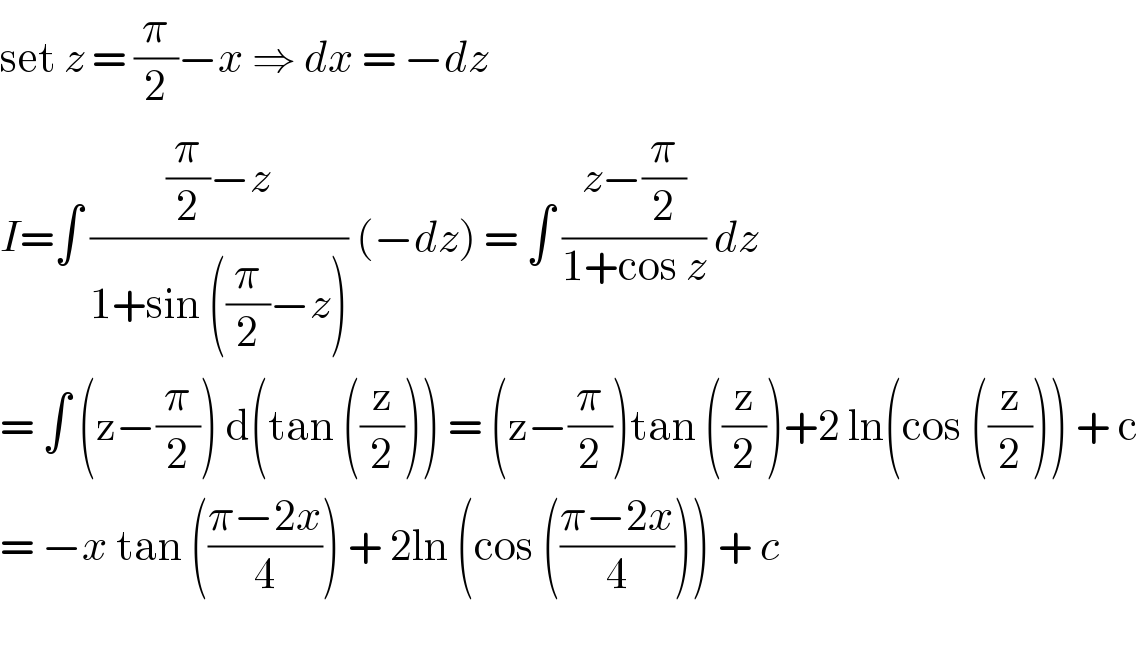
set z = (π/2)−x ⇒ dx = −dz I=∫ (((π/2)−z)/(1+sin ((π/2)−z))) (−dz) = ∫ ((z−(π/2))/(1+cos z)) dz = ∫ (z−(π/2)) d(tan ((z/2))) = (z−(π/2))tan ((z/2))+2 ln(cos ((z/2))) + c = −x tan (((π−2x)/4)) + 2ln (cos (((π−2x)/4))) + c

$$\mathrm{set}\:{z}\:=\:\frac{\pi}{\mathrm{2}}−{x}\:\Rightarrow\:{dx}\:=\:−{dz} \\ $$$${I}=\int\:\frac{\frac{\pi}{\mathrm{2}}−{z}}{\mathrm{1}+\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}−{z}\right)}\:\left(−{dz}\right)\:=\:\int\:\frac{{z}−\frac{\pi}{\mathrm{2}}}{\mathrm{1}+\mathrm{cos}\:{z}}\:{dz} \\ $$$$=\:\int\:\left(\mathrm{z}−\frac{\pi}{\mathrm{2}}\right)\:\mathrm{d}\left(\mathrm{tan}\:\left(\frac{\mathrm{z}}{\mathrm{2}}\right)\right)\:=\:\left(\mathrm{z}−\frac{\pi}{\mathrm{2}}\right)\mathrm{tan}\:\left(\frac{\mathrm{z}}{\mathrm{2}}\right)+\mathrm{2}\:\mathrm{ln}\left(\mathrm{cos}\:\left(\frac{\mathrm{z}}{\mathrm{2}}\right)\right)\:+\:\mathrm{c} \\ $$$$=\:−{x}\:\mathrm{tan}\:\left(\frac{\pi−\mathrm{2}{x}}{\mathrm{4}}\right)\:+\:\mathrm{2ln}\:\left(\mathrm{cos}\:\left(\frac{\pi−\mathrm{2}{x}}{\mathrm{4}}\right)\right)\:+\:{c} \\ $$$$ \\ $$

Commented by bemath last updated on 01/Jul/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{both} \\ $$

Answered by smridha last updated on 01/Jul/20

∫((x(1−sinx))/((1+sinx)(1−sinx)))dx =∫xsec^2 x dx−∫xtanx.secx dx =xtanx+ln[cosx]−xsecx+ln[tan{(𝛑/4)+(x/2)}]+c or =x(tanx−secx)−ln(secx)+ln[secx+tanx]+c

$$\int\frac{\boldsymbol{{x}}\left(\mathrm{1}−\boldsymbol{{sinx}}\right)}{\left(\mathrm{1}+\boldsymbol{{sinx}}\right)\left(\mathrm{1}−\boldsymbol{{sinx}}\right)}\boldsymbol{{dx}} \\ $$$$=\int\boldsymbol{{xsec}}^{\mathrm{2}} \boldsymbol{{x}}\:\boldsymbol{{dx}}−\int\boldsymbol{{xtanx}}.\boldsymbol{{secx}}\:\boldsymbol{{dx}} \\ $$$$=\boldsymbol{{xtanx}}+\boldsymbol{{ln}}\left[\boldsymbol{{cosx}}\right]−\boldsymbol{{xsecx}}+\boldsymbol{{ln}}\left[\boldsymbol{{tan}}\left\{\frac{\boldsymbol{\pi}}{\mathrm{4}}+\frac{\boldsymbol{{x}}}{\mathrm{2}}\right\}\right]+\boldsymbol{{c}} \\ $$$$\boldsymbol{{or}}\: \\ $$$$=\boldsymbol{{x}}\left(\boldsymbol{{tanx}}−\boldsymbol{{secx}}\right)−\boldsymbol{{ln}}\left(\boldsymbol{{secx}}\right)+\boldsymbol{{ln}}\left[\boldsymbol{{secx}}+\boldsymbol{{tanx}}\right]+\boldsymbol{{c}} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply