Menu Close

x-1-x-1-x-1-x-1-dx-

Tinku Tara 0 Comments
Pin




Question Number 65015 by aliesam last updated on 24/Jul/19
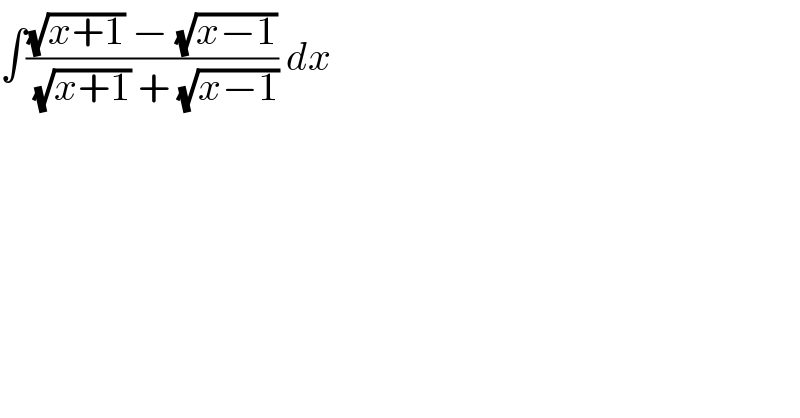
∫(((√(x+1)) − (√(x−1)))/( (√(x+1)) + (√(x−1)))) dx
$$\int\frac{\sqrt{{x}+\mathrm{1}}\:−\:\sqrt{{x}−\mathrm{1}}}{\:\sqrt{{x}+\mathrm{1}}\:+\:\sqrt{{x}−\mathrm{1}}}\:{dx} \\ $$
Commented by mathmax by abdo last updated on 24/Jul/19
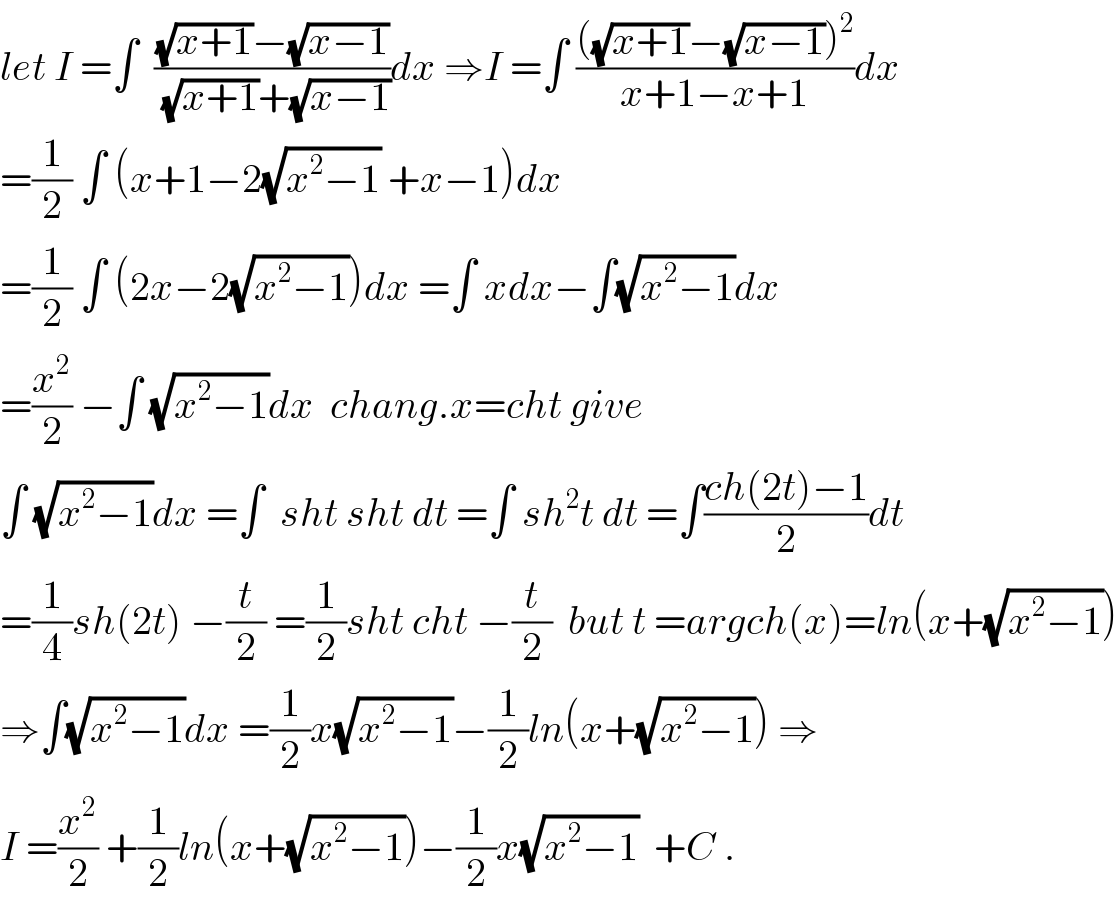
let I =∫ (((√(x+1))−(√(x−1)))/( (√(x+1))+(√(x−1))))dx ⇒I =∫ ((((√(x+1))−(√(x−1)))^2 )/(x+1−x+1))dx =(1/2) ∫ (x+1−2(√(x^2 −1)) +x−1)dx =(1/2) ∫ (2x−2(√(x^2 −1)))dx =∫ xdx−∫(√(x^2 −1))dx =(x^2 /2) −∫ (√(x^2 −1))dx chang.x=cht give ∫ (√(x^2 −1))dx =∫ sht sht dt =∫ sh^2 t dt =∫((ch(2t)−1)/2)dt =(1/4)sh(2t) −(t/2) =(1/2)sht cht −(t/2) but t =argch(x)=ln(x+(√(x^2 −1))) ⇒∫(√(x^2 −1))dx =(1/2)x(√(x^2 −1))−(1/2)ln(x+(√(x^2 −1))) ⇒ I =(x^2 /2) +(1/2)ln(x+(√(x^2 −1)))−(1/2)x(√(x^2 −1)) +C .
$${let}\:{I}\:=\int\:\:\frac{\sqrt{{x}+\mathrm{1}}−\sqrt{{x}−\mathrm{1}}}{\:\sqrt{{x}+\mathrm{1}}+\sqrt{{x}−\mathrm{1}}}{dx}\:\Rightarrow{I}\:=\int\:\frac{\left(\sqrt{{x}+\mathrm{1}}−\sqrt{{x}−\mathrm{1}}\right)^{\mathrm{2}} }{{x}+\mathrm{1}−{x}+\mathrm{1}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\left({x}+\mathrm{1}−\mathrm{2}\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\:+{x}−\mathrm{1}\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\left(\mathrm{2}{x}−\mathrm{2}\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\right){dx}\:=\int\:{xdx}−\int\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}{dx} \\ $$$$=\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:−\int\:\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}{dx}\:\:{chang}.{x}={cht}\:{give} \\ $$$$\int\:\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}{dx}\:=\int\:\:{sht}\:{sht}\:{dt}\:=\int\:{sh}^{\mathrm{2}} {t}\:{dt}\:=\int\frac{{ch}\left(\mathrm{2}{t}\right)−\mathrm{1}}{\mathrm{2}}{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}{sh}\left(\mathrm{2}{t}\right)\:−\frac{{t}}{\mathrm{2}}\:=\frac{\mathrm{1}}{\mathrm{2}}{sht}\:{cht}\:−\frac{{t}}{\mathrm{2}}\:\:{but}\:{t}\:={argch}\left({x}\right)={ln}\left({x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\right) \\ $$$$\Rightarrow\int\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}{x}\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\right)\:\Rightarrow \\ $$$${I}\:=\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\right)−\frac{\mathrm{1}}{\mathrm{2}}{x}\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\:\:+{C}\:. \\ $$
Commented by aliesam last updated on 24/Jul/19
thank you sir
$${thank}\:{you}\:{sir} \\ $$
Commented by mathmax by abdo last updated on 24/Jul/19
you are welcome.
$${you}\:{are}\:{welcome}. \\ $$
Answered by Tanmay chaudhury last updated on 24/Jul/19
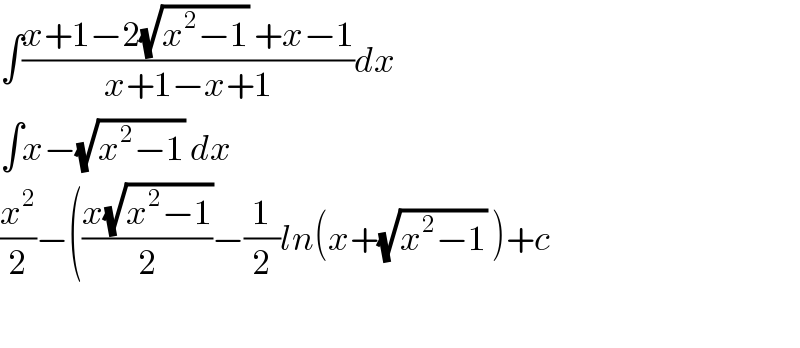
∫((x+1−2(√(x^2 −1)) +x−1)/(x+1−x+1))dx ∫x−(√(x^2 −1)) dx (x^2 /2)−(((x(√(x^2 −1)))/2)−(1/2)ln(x+(√(x^2 −1)) )+c
$$\int\frac{{x}+\mathrm{1}−\mathrm{2}\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\:+{x}−\mathrm{1}}{{x}+\mathrm{1}−{x}+\mathrm{1}}{dx} \\ $$$$\int{x}−\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\:{dx} \\ $$$$\frac{{x}^{\mathrm{2}} }{\mathrm{2}}−\left(\frac{{x}\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\:\right)+{c}\right. \\ $$$$ \\ $$
Commented by aliesam last updated on 24/Jul/19
thank you sir
$${thank}\:{you}\:{sir} \\ $$
Commented by Tanmay chaudhury last updated on 24/Jul/19
most welcome sir
$${most}\:{welcome}\:{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *