Question Number 123494 by bemath last updated on 25/Nov/20
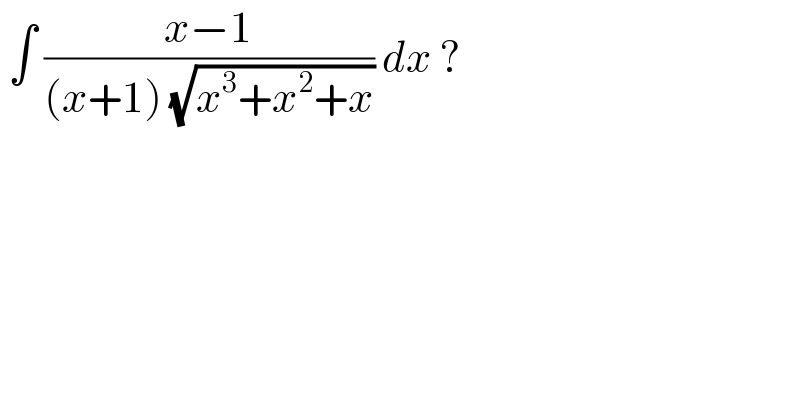
$$\:\int\:\frac{{x}−\mathrm{1}}{\left({x}+\mathrm{1}\right)\:\sqrt{{x}^{\mathrm{3}} +{x}^{\mathrm{2}} +{x}}}\:{dx}\:? \\ $$
Answered by bramlexs22 last updated on 26/Nov/20
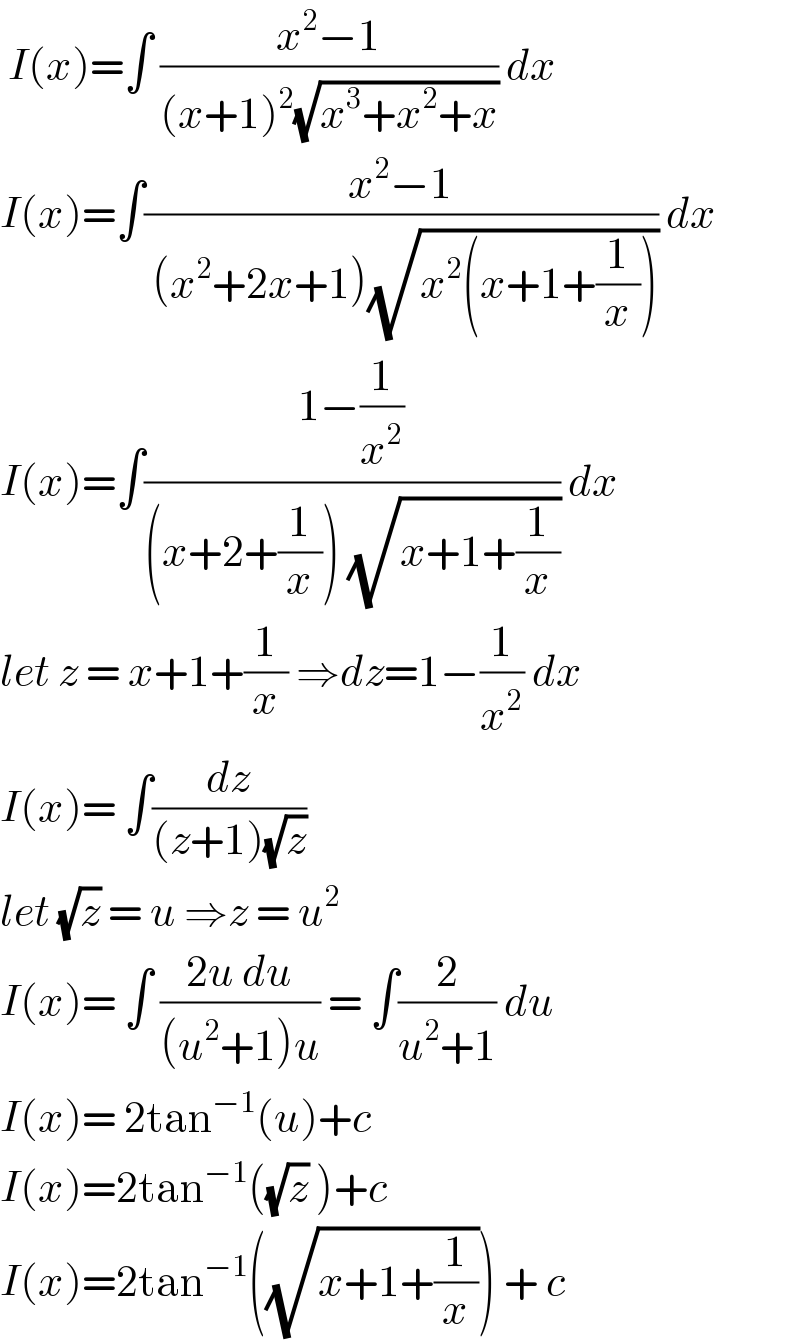
$$\:{I}\left({x}\right)=\int\:\frac{{x}^{\mathrm{2}} −\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} \sqrt{{x}^{\mathrm{3}} +{x}^{\mathrm{2}} +{x}}}\:{dx} \\ $$$${I}\left({x}\right)=\int\frac{{x}^{\mathrm{2}} −\mathrm{1}}{\:\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} \left({x}+\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)}}\:{dx} \\ $$$${I}\left({x}\right)=\int\frac{\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{\left({x}+\mathrm{2}+\frac{\mathrm{1}}{{x}}\right)\:\sqrt{{x}+\mathrm{1}+\frac{\mathrm{1}}{{x}}}}\:{dx} \\ $$$${let}\:{z}\:=\:{x}+\mathrm{1}+\frac{\mathrm{1}}{{x}}\:\Rightarrow{dz}=\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:{dx} \\ $$$${I}\left({x}\right)=\:\int\frac{{dz}}{\left({z}+\mathrm{1}\right)\sqrt{{z}}}\: \\ $$$${let}\:\sqrt{{z}}\:=\:{u}\:\Rightarrow{z}\:=\:{u}^{\mathrm{2}} \\ $$$${I}\left({x}\right)=\:\int\:\frac{\mathrm{2}{u}\:{du}}{\left({u}^{\mathrm{2}} +\mathrm{1}\right){u}}\:=\:\int\frac{\mathrm{2}}{{u}^{\mathrm{2}} +\mathrm{1}}\:{du} \\ $$$${I}\left({x}\right)=\:\mathrm{2tan}^{−\mathrm{1}} \left({u}\right)+{c}\: \\ $$$${I}\left({x}\right)=\mathrm{2tan}^{−\mathrm{1}} \left(\sqrt{{z}}\:\right)+{c} \\ $$$${I}\left({x}\right)=\mathrm{2tan}^{−\mathrm{1}} \left(\sqrt{{x}+\mathrm{1}+\frac{\mathrm{1}}{{x}}}\right)\:+\:{c}\: \\ $$
Commented by liberty last updated on 26/Nov/20

$${good} \\ $$
Commented by liberty last updated on 26/Nov/20
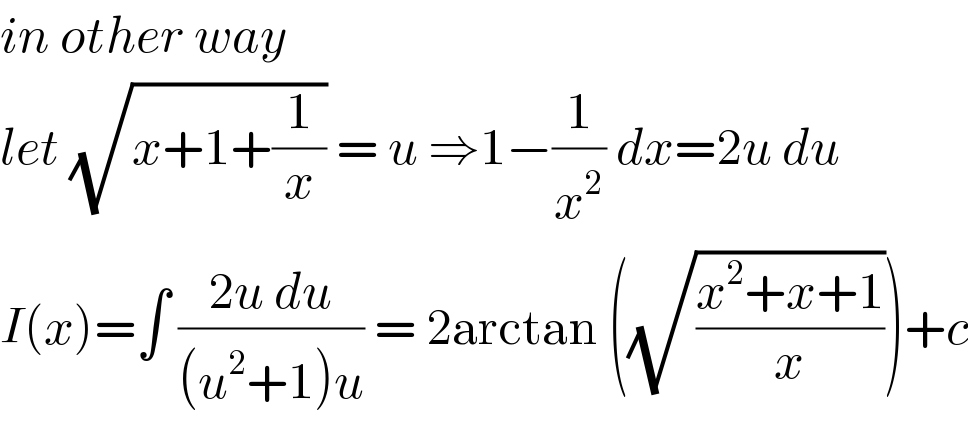
$${in}\:{other}\:{way} \\ $$$${let}\:\sqrt{{x}+\mathrm{1}+\frac{\mathrm{1}}{{x}}}\:=\:{u}\:\Rightarrow\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:{dx}=\mathrm{2}{u}\:{du} \\ $$$${I}\left({x}\right)=\int\:\frac{\mathrm{2}{u}\:{du}}{\left({u}^{\mathrm{2}} +\mathrm{1}\right){u}}\:=\:\mathrm{2arctan}\:\left(\sqrt{\frac{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{{x}}}\right)+{c} \\ $$
Commented by MJS_new last updated on 26/Nov/20
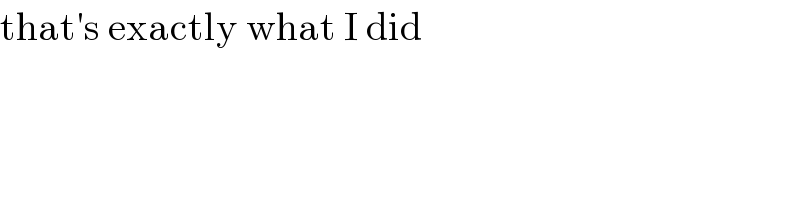
$$\mathrm{that}'\mathrm{s}\:\mathrm{exactly}\:\mathrm{what}\:\mathrm{I}\:\mathrm{did} \\ $$
Answered by MJS_new last updated on 26/Nov/20
![∫((x−1)/((x+1)(√(x(x^2 +x+1)))))dx= [t=((√(x^2 +x+1))/( (√x))) → dx=((2x^(3/2) (√(x^2 +x+1)))/(x^2 −1))] =2∫(dt/(t^2 +1))=2arctan t =2arctan ((√(x^2 +x+1))/( (√x))) +C](https://www.tinkutara.com/question/Q123499.png)
$$\int\frac{{x}−\mathrm{1}}{\left({x}+\mathrm{1}\right)\sqrt{{x}\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}{\:\sqrt{{x}}}\:\rightarrow\:{dx}=\frac{\mathrm{2}{x}^{\mathrm{3}/\mathrm{2}} \sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}{{x}^{\mathrm{2}} −\mathrm{1}}\right] \\ $$$$=\mathrm{2}\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}=\mathrm{2arctan}\:{t}\:=\mathrm{2arctan}\:\frac{\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}{\:\sqrt{{x}}}\:+{C} \\ $$
Commented by bramlexs22 last updated on 26/Nov/20
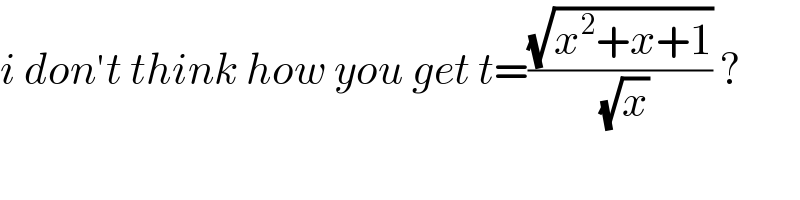
$${i}\:{don}'{t}\:{think}\:{how}\:{you}\:{get}\:{t}=\frac{\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}{\:\sqrt{{x}}}\:? \\ $$
Commented by MJS_new last updated on 26/Nov/20
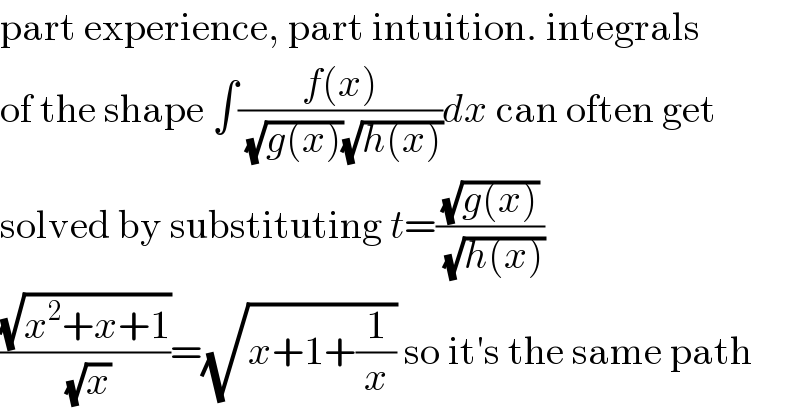
$$\mathrm{part}\:\mathrm{experience},\:\mathrm{part}\:\mathrm{intuition}.\:\mathrm{integrals} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{shape}\:\int\frac{{f}\left({x}\right)}{\:\sqrt{{g}\left({x}\right)}\sqrt{{h}\left({x}\right)}}{dx}\:\mathrm{can}\:\mathrm{often}\:\mathrm{get} \\ $$$$\mathrm{solved}\:\mathrm{by}\:\mathrm{substituting}\:{t}=\frac{\sqrt{{g}\left({x}\right)}}{\:\sqrt{{h}\left({x}\right)}} \\ $$$$\frac{\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}{\:\sqrt{{x}}}=\sqrt{{x}+\mathrm{1}+\frac{\mathrm{1}}{{x}}}\:\mathrm{so}\:\mathrm{it}'\mathrm{s}\:\mathrm{the}\:\mathrm{same}\:\mathrm{path} \\ $$
Commented by bramlexs22 last updated on 26/Nov/20
$${oo}\:{thank}\:{you}\:{sir}\:{for}\:{your}\:{sharing} \\ $$
