Question Number 85839 by sahnaz last updated on 25/Mar/20
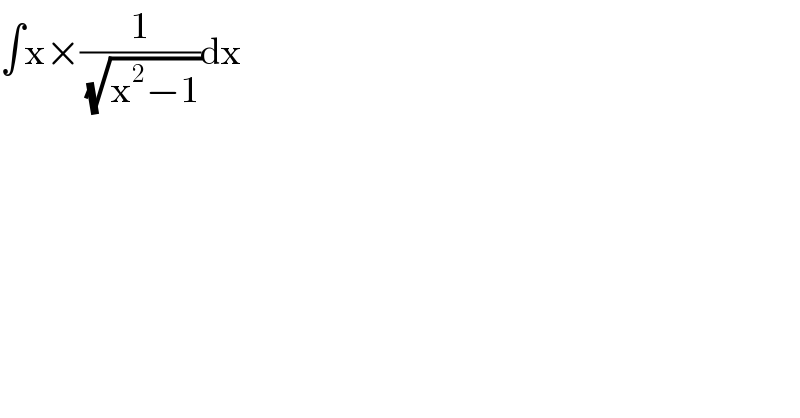
$$\int\mathrm{x}×\frac{\mathrm{1}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}}\mathrm{dx} \\ $$
Commented by jagoll last updated on 25/Mar/20
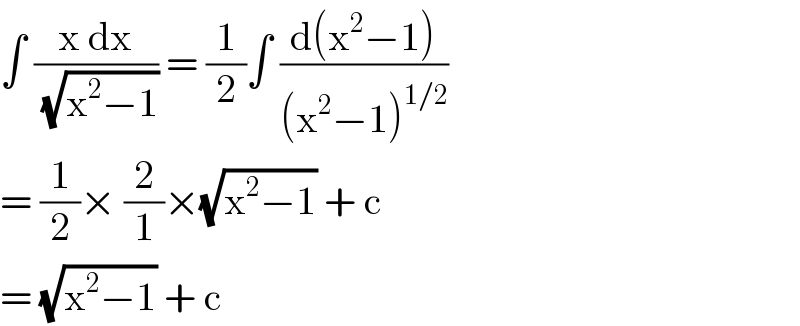
$$\int\:\frac{\mathrm{x}\:\mathrm{dx}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{d}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{1}/\mathrm{2}} } \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}×\:\frac{\mathrm{2}}{\mathrm{1}}×\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\:+\:\mathrm{c} \\ $$$$=\:\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\:+\:\mathrm{c}\: \\ $$
Answered by sakeefhasan05@gmail.com last updated on 25/Mar/20
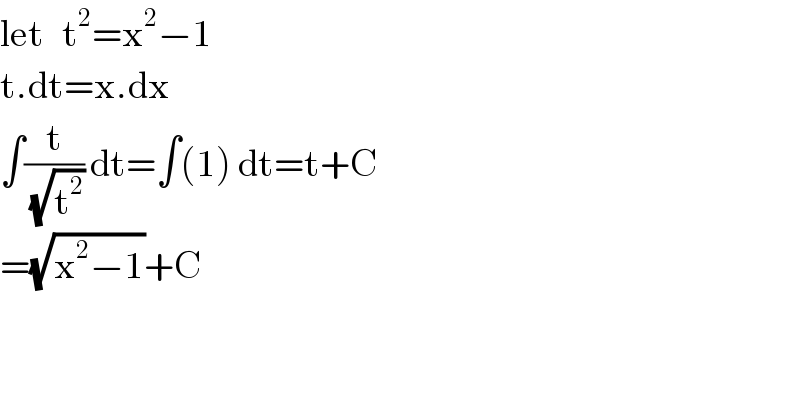
$$\mathrm{let}\:\:\:\mathrm{t}^{\mathrm{2}} =\mathrm{x}^{\mathrm{2}} −\mathrm{1} \\ $$$$\mathrm{t}.\mathrm{dt}=\mathrm{x}.\mathrm{dx} \\ $$$$\int\frac{\mathrm{t}}{\:\sqrt{\mathrm{t}^{\mathrm{2}} }}\:\mathrm{dt}=\int\left(\mathrm{1}\right)\:\mathrm{dt}=\mathrm{t}+\mathrm{C} \\ $$$$=\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}+\mathrm{C} \\ $$$$ \\ $$$$ \\ $$
